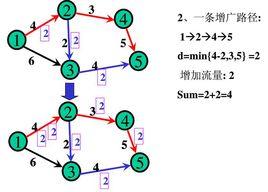
發現簡史
最大流問題是一類套用極為廣泛的問題,例如在交通網路中有人流、車流、貨物流,供水網路中有水流,金融系統中現金流,等等。求最大流的標號算法最早由福特和福克遜於1956年提出,20世紀50年代福特(Ford)、福克遜(Fulkerson)建立的“網路流理論”,是網路套用的重要組成成分。
數學模型
最大流問題,是網路流理論研究的一個基本問題,求網路中一個可行流f*,使其流量v(f)達到最大, 這種流f稱為最大流,這個問題稱為(網路)最大流問題。最大流問題是一個特殊的線性規劃問題,就是在容量網路中,尋找流量最大的可行流。
最大流問題可以建立如下形式的線性規劃數學模型:
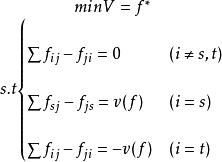 最大流問題
最大流問題式中v(f)稱為這個可行流的流量、發點的淨輸出量或收點的淨輸出量。∞一般用標號法尋求有向最大流比用求線性規劃問題的一般方法要方便得多。
最大的標號算法還用於解決多發點多收點網路的最大問題,設容量網路G有若干個發點x,x,...,x;若干收點y,y,...,y,可以添加兩個新點vs,vt,用容量為∞的有向邊分別連線兩個新點v與點x,x,...,x,點y,y,...,y與v,得到新的網路G‘。G’是一個只有一個收點和發點的網路,求解最大流問題即可都得到G的解。
網路流概念
圖和收發點
一個圖是由點集V={v}和V中元素的無序對的一個集合E={e}所構成的二元組,記為G=(V,E),V中的元素v叫做頂點,E中的元素e,叫做邊。
僅有一個入次為0的點v稱為發點(源),一個出次為0的點v稱為收點(匯),其餘點為中間點,這樣的網路G稱為容量網路,常記做G=(V,E,C)。
容量和流量
 最大流問題
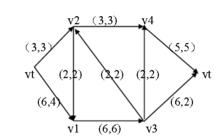
最大流問題設有向連通圖G=(V,E),G的每條邊(v,v)上的非負數c稱為邊的容量。對任一G中的邊(v,v)有流量f,稱集合f={f}為網路G上的一個流。右圖即為一個有向連通圖,括弧中第一個數字代表容量,第二個數字代表流量。
可行流
稱滿足下列兩個條件的流為可行流:
1.容量限制條件:對G中的每條邊(v,v),有0≤f≤c;即每條邊上的流量非負而且最大也只能達到容量的限制。
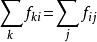 最大流問題
最大流問題2.平衡條件:對中間點v,有 ,即物資的輸入量和輸出量相等。
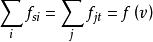 最大流問題
最大流問題對發、收點v,v,,有 ,f為網路流的總流量。
一個流f={f},當f=c,則稱流f對邊(vi,vj)是飽和的,否則稱f對(v,v)不飽和。
割(截)集
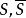 最大流問題
最大流問題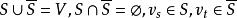 最大流問題
最大流問題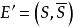 最大流問題
最大流問題容量網路G=(V,E,C),v,v為發、收點,若有邊集E‘為E的子集,將G為兩個子圖G,G,即點集V被剖分其為兩個頂點集合分別記 ,必有 。若有邊集E'為E的子集,滿足下列兩個的性質,則稱E’為G的割集(也稱截集),記 。
1.若把整個截集的弧從網路G=(V,E,C)中丟去,則不存在從v和vt的有向路,即圖(V,E-E')不連通。
2.只要沒把整個截集刪去,就存在從v和vt的有向路,即當E’‘為E的真子集,圖G(V,E-E'')仍連通。
由此可知,截集是從起點v到終點v的必經之路。
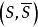 最大流問題
最大流問題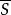 最大流問題
最大流問題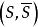 最大流問題
最大流問題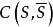 最大流問題
最大流問題割集 中所有始點在S,終點在 的邊的容量之和,稱為 的割集容量,記為 。容量網路G的割集有很多個,其中割集容量最小這成為網路G的最小割集容量(簡稱最小割)。
最小割定理
由割集的定義不難看出,無論拿掉那個割集,發點v到收點v便不再相通,所以任何一個可行流都會經過割集,且不會超過任一割集的容量。最小割如同瓶頸一般,即使是最大流也無法超過最小割,網路的最大流與最小割容量滿足下面的定理(證明略)。
定理一
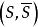 最大流問題
最大流問題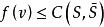 最大流問題
最大流問題設f為網路G=(V,E,C)的任一可行流,流量為v(f), 是分離v,v的任一割集,則有 。
定理二
由定理一可知,最大流的流量v(f)和某一割集K的容量相等,而且最大流的流量本身也不帶任一割集的容量,因此割集一定是最小的割集。
任一網路G中,從v到v的最大流的流量等於分離v、v的最小割的容量(最小的割集的容量)。
前後向弧
一條從起點v到終點vt的鏈μ,規定從v到v的方向為鏈μ的方向,鏈上與μ方向一致的邊叫前向弧(邊),記作μ ;與μ方向相反的邊稱為後向弧(邊),記作μ 。
可增廣鏈
f是一個可行流,f表示由i點指向j點的流量,如果滿足前向弧的流量非負且小於容量,或後向弧的流量大於0且不超過容量:
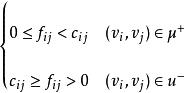 最大流問題
最大流問題則稱μ為從v到v的關於f的可增廣鏈。
可增廣鏈的實際意義是:沿著這條從v到v輸送的流,仍有潛力可挖,只要前向弧的流量增加或後向弧的流量減少,就可以將截集的流量提高。調整後的流,在各點仍滿足平衡條件及容量限制條件,仍為可行流。
從另一個角度來說,可以提高流量的可行流也不是最大流,因此可行流f是最大流的充要條件是不存在從v到v的可增廣鏈。
標號算法
算法思路
從可行流和可增廣鏈關係來看,就可以知道一種尋求最大流的方法:從一個可行流開始,尋求關於這個可行流的可增廣鏈,若存在,則可以經過調整,得到一個新的可行流,其流量比原來的可行流要大,重複這個過程,直到不存在關於該流的可增廣鏈時就得到了最大流。 v這種算法由Ford 和 Fulkerson於1956年提出,故又稱 Ford-Fulkerson標號法。
算法步驟
標號的方法可分為兩步:第一步是標號過程,通過標號來尋找可增廣鏈;第二步是調整過程,沿可增廣連調整f以增加流量。
1.標號過程
(1)給發點(始點)以標號(△,+∞)或(0,+∞)。
(2)選擇一個已標號的頂點v,對於v的所有未給標號的鄰接點v按下列規則處理:
(a)若後向邊(v,v)∈E,且f>0時,則令δ=min(f,δ),並給v以標號(-v,δ),這表明v點的v點的邊最多可以減少δ的流量以提高整個網路的流量。
(b)若前向邊(v,v)∈E,且f>c時,令δ=min(c-f,δ),並給v以標號(+v,δ),這表明v點到v點的邊最多可以增加δ的流量以提高整個網路的流量。
括弧內的第一個數字表示這個節點得到的得到標號前的第一個結點的代號,第二個數字表示從上個標號節點到這個標號節點允許的最大調整量δ,假定發點的調整量不限,所以標記為+∞。
(3)重複(2)直到收點v被標號或不再有頂點可被標號為止。
若v沒有得到標號,說明標號過程已無法進行,可行流f已是最大流。若v得到標號,說明存在一條可增廣鏈,轉入調整過程。標號若有多條增廣鏈時,不用刻意考慮哪種調整更適合,只需一條一條地轉入調整過程,不用全盤考慮。
2.調整過程
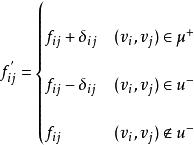 最大流問題
最大流問題(1)令這條被找到的增廣鏈中所有的前向弧全部加上δ的流量,所有的後向弧全部減去δ的流量,至於不在增廣鏈之中的邊的流量則不需要調整。
(2)去掉所有標號,回到第1步,對可行流f’重新標號。