可公度性
美元指數可公度性的觀察可公度性是自然界的一種秩序。“可公度性”一詞是在天文學中首先提出來的。拉普拉斯在200多年前注意到木星的三個主要衛星的平均運動Z1，Z2，Z3服從下列關係式：Z1-3×Z2+2×Z3=0。同樣，土星的四個衛星的平均運動Y1，Y2，Y3，Y4也具有類似的關係：5×Y1-10×Y2+Y3+4×Y4=0。我們就稱這些衛星之間存在可公度性。由於至今還沒有人能夠提出有說服力的機制理論，所以一直當作經驗關係寫入某些文獻中。筆者認為可公度性的實質是——利用數學模式反映出事物本身或相關事物之間的運動關係中隱含的周期性規律，它是周期性規律的擴張化套用，在增加錯誤（或虛驚）機率的代價下，可以從很寬的範圍內分辨並抽提出微弱的、非偶然的信號，類似於遺傳算法中的自我隔代複製。
除了天文學，自然界的許多客觀事物都存在著可公度性。
化學元素周期表
我們從化學元素周期表取出前10個元素，按原子量順序排，得出：
X1(H)=1.008，X2(He)=4.003,X3(Li)=6.941，X4(Be)=9.012，X5(B)=10.811，X6(C)=12.011，X7(N)=14.0067，X8(O)=16.000，X9(F)=18.998，X10(Ne)=20.179。
它們之間的可公度性二元公式具有以下關係：
X1+X6=13.019，幾乎等於X2+X4=13.015；
X1+X9=20.006，幾乎等於X2+X8=20.003；
X4+X9=28.010，幾乎等於X6+X8=28.011，X7+X7=28.014。
它們之間的五元可公度性可表達為：
X9+X9+X1-X6-X2=22.99
X9+X8+X1-X4-X2=22.991
X9+X7+X7-X6-X6=22.9894
X8+X8+X4-X7-X2=23.0023
X6+X4+X2-X1-X1=23.01
它們的值都幾乎與鈉（Na）的實際原子量22.98接近，可信度達到99%。
2．可公度性在氣象災變預測中也得到了非常廣泛的運用，曾經有人預測北京每年的大風大雨時間，準確率在80%以上。可公度性在地震預測中的實用性也非常強。
3．可公度性的概念從天文學擴張到統計預測學中。
在經典統計學中，對擲硬幣有一個不可動搖的定論：擲的次數越多，正面和反面越傾向於平均。如擲100次，正面的次數為53，反面的次數為47，正面53%，反面47%；當擲到1000次時，正面的次數可能只有520，反面的次數只有480，正面52%，反面48%——擲的次數越多，正面和反面比例上越趨同。這一經典結論自從產生後未受到任何人的懷疑。其實，我們如果從差異性來分析，可以看到，如果你擲100次，正面的次數比反面的次數多6次，而當你擲1000次，正面的次數已經比反面的次數多40次了，這說明兩者之間的差隨著擲的次數增多，不是減少而是增大，因此，實際運用統計學原理時不僅要研究數的平均，還要研究數的差，筆者認為可公度性正是研究數的和與差。
從這一思維起點出發，我們可以認為數學模式是自然模式的反映，但是：
1）自然模式里也存在著偶然性和普適性，偶然性事件的發生不具有可重複性，無法反覆驗證，缺乏可公度性。普適性事件不僅時有發生，而且還會以某些特定的方式重複出現，具有一定的規律性，可以建立某種數學模式，分析過去並預測未來。
2）作為對自然模式的反映，數學模式並不是越複雜越好。
3）只有越簡單才越具有普適性，越能反映自然模式，加減法最能保持自然數的完整性，儘可能準確地反映了自然的本性，可公度性預測方法裡只有加和減，這將大大增加它的普適性。
4）經典統計學之所以在實際運用中效果較差，主要就是它只強調了平均數，而忽略了自然運動的多變性和事物在周期性演變中的離差現象。可公度性的預測方法主要是對離差現象的研究。
股市中的預測
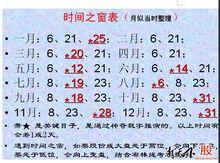時間之窗例如大家都知道上證指數的一個主要低點循環周期是18-20個月，除此之外還隱藏哪些周期，一時半會還不容易發現，而且當大部分人都在利用這個數據時，它的有效性就大打折扣，按以前的規律。我們利用可公度性對上證指數進行中遠期重要轉折點預測，得到非常好的效果，以下為預測方法。
選點問題
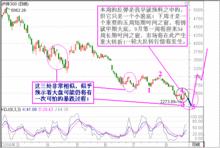利用時間之窗預測股市未來走勢首先解決選點問題，根據混沌理論中的分形理論原理，底部轉折點的前一點和後一點均比轉折點高，頂部轉折點的前一點和後一點均比轉折點低。其次，起點取上證指數歷史上第一個重要的轉折點。另由於上證指數第一個交易日為1990年12月19日，所以月份的劃分以每月18日為界。
低點的可公度性
以下為1991年5月18日上證指數104點以來歷次主要低點的時間跨度表，計算方式如下：
設1991年5月18日為0點，低點時間在當月18日之前的計算方法為
時間跨度=（年份-1991）×12-5+月份
低點時間在當月18日之後的只要再加上1即可。
| 序號 | 指數時間（點位） | 時間跨度 | 序號 | 指數時間（點位） | 時間跨度 |
| X0 | 1991.05.17（104） | 0 | X14 | 1999.12.27（1341） | 104 |
| X1 | 1992.11.17（386） | 18 | X15 | 2000.09.25（1874） | 113 |
| X2 | 1993.03.25（913） | 23 | X16 | 2001.02.22（1893） | 118 |
| X3 | 1993.07.27（777） | 27 | X17 | 2001.10.22（1514） | 126 |
| X4 | 1993.10.25（774） | 30 | X18 | 2002.01.29（1339） | 129 |
| X5 | 1994.07.29（325） | 39 | X19 | 2002.06.06（1455） | 133 |
| X6 | 1995.02.07（524） | 45 | X20 | 2003.01.06（1311） | 140 |
| X7 | 1995.07.04（610） | 50 | X21 | 2003.11.13（1307） | 150 |
| X8 | 1996.01.19（512） | 56 | X22 | 2004.09.13（1259） | 160 |
| X9 | 1996.12.25（855） | 68 | X23 | 2005.02.01（1187） | 165 |
| X10 | 1997.09.23（1025） | 77 | X24 | 2005.06.03（998） | 169 |
| X11 | 1998.08.18（1043） | 87 | X25 | 2005.07.11（1004） | 170 |
| X12 | 1999.02.08（1064） | 93 | X26 | 2005.10.28（1067） | 174 |
| X13 | 1999.05.17（1047） | 96 |
我們看到X20以前數據基本上可以找到可公度性的規律，比如：
1）X20的低點可以根據以下二元公式數據組得出：
X2+X16=23+118=141，X3+X15=27+113=140，X6+X13=45+96=141，
X19的低點可以根據以下二元公式數據組得出：
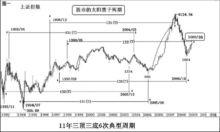太陽月周期與月亮周期組合成時間之窗X4+X14=30+104=134，X5+X12=39+93=132，X6+X11=45+87=132，X8+X10=56+77=133
2）其他數據也可以根據類似的方法找出，根據以上低點數據目前我們採用二元公式，即把數字兩兩相加，得出如下數據組：
X4+X15=30+113=143，X5+X14=39+104=143，X8+X11=56+87=143，X1+X17=18+126=144
143指向03年3月，144指向03年4月，也就是說今年2003年3－4月有可能出現一個低點或者次低點。
3）另外我們可以看到另一組數據：
X1+X19=18+133=151，X2+X18=23+129=152，X5+X15=39+113=152，X8+X13=56+96=152，
152指向03年2003年12月附近，也就是說03年底有可能出現另一個低點。意味著我們在03年底之前要選擇高點時間區做一次全面的減倉出貨。
4）X26低點可以根據以下二元公式數據組得出：
X2+X21=23+150=173，X6+X18=45+129=174，X8+X16=56+118=174，X10+X13=77+96=173
可見 2005.10.28 也是全年一個重要的時間拐點喔。
5）07年大牛市可以根據以下二元公式數據組得出：
X1+X25=18+170=188，X2+X23=23+165=188，X3+X22=27+160=187，
X5+X21=39+150=189，X8+X19=56+133=189
188指向2006年12月附近，年底可能出現個時間拐點，12月或許是大級別的低點時間窗。
同樣X6+X20=45+140=185，X8+X18=56+129=185。185指向2006年9月，也可能是一個低點。
高點的可公度性
計算方式如下：
設1992年5月24日為0點，高點時間在當月18日之前的計算方法為
時間跨度=（年份-1992）×12-5+月份-1
高點時間在當月18日之後的只要不減1即可。
| 序號 | 指數時間（點位） | 時間跨度 | 序號 | 指數時間（點位） | 時間跨度 |
| X0 | 1992.05.24（1429） | 0 | X14 | 1999.06.30（1756） | 85 |
| X1 | 1993.02.16（1558） | 8 | X15 | 1999.09.10（1695） | 87 |
| X2 | 1993.04.29（1392） | 11 | X16 | 2000.08.22（2114） | 99 |
| X3 | 1993.08.17（1042） | 15 | X17 | 2001.01.08（2131） | 103 |
| X4 | 1993.12.08（1044） | 18 | X18 | 2001.06.14（2245） | 108 |
| X5 | 1994.09.13（1052） | 27 | X19 | 2001.12.05（1776） | 114 |
| X6 | 1995.05.22（927） | 36 | X20 | 2002.03.21（1693） | 118 |
| X7 | 1995.09.12（790） | 39 | X21 | 2002.06.25 (1748) | 121 |
| X8 | 1996.07.24（894） | 50 | X22 | 2003.04.16（1650） | 130 |
| X9 | 1996.12.11（1258） | 54 | X23 | 2004.04.07（1783） | 143 |
| X10 | 1997.05.12（1510） | 59 | X24 | 2004.09.24（1496） | 148 |
| X11 | 1997.09.11（1264） | 63 | X25 | 2005.02.25（1328） | 153 |
| X12 | 1998.06.04（1422） | 72 | X26 | 2005.06.09（1146） | 156 |
| X13 | 1998.11.17（1300） | 77 | X27 | 2005.09.20（1224） | 160 |
首先，我們可以看到以前的數據基本上可以找到可公度性的規律，比如：
1）X21的高點可以根據以下二元公式數據組得出：
X1+X19=8+114=122，X4+X17=18+103=121，X6+X14=36+85=121，
X8+X12=50+72=122，X10+X11=59+63=122
有這么多的時間周期匯集，難怪2002年的六、七月份是鐵頂，
2）X20的高點可以根據以下二元公式數據組得出：
X2+X18=11+108=119，X3+X17=15+103=118，X4+X16=18+99=117，
X9+X11=54+63=117，X10+X10=59+59=118
3）其次根據以上高點數據我們採用二元公式，即把數字兩兩相加，得出如下數據組：
X1+X21=8+121=129，X2+X20=11+118=129，X3+X19=15+114=129，X5+X17=27+103=130，
129指向2003年2月附近，所以2003年2月在高位反覆震盪都無法向上突破。
4）2003下一個重要高點數據指向哪呢？看看以下數據組：
X2+X21=11+121=132，X3+X20=15+118=133，X4+X19=18+114=132，
X9+X13=54+77=131，X10+X12=59+72=131，
131指向2003年4月，132指向2003年5月，也就是說2003年4—5月有可能出現一個高點。
5）另一個數據組：
X4+X20=18+118=136，X5+X18=27+108=135，X6+X16=36+99=135，
X8+X14=50+85=135，X10+X13=59+77=136，X11+X12=63+72=135
135指向2003年8月，136指向2003年9月，也就是說今年8—9月有可能出現一個重要高點或者次高點。如果在那時還有股票的朋友需要特別小心了。結合上次預測的低點信號，我們認為2003年第四季度股票持倉率應相對保守。
6）另一個數據組：
X1+X27=8+160=168 ，X2+X26=11+156=167 ，X3+X25=15+153=168 ，
X8++X20=50+118=168， X9+X19=54+114=168
168指向2006年5月份 所以小寶認為是一個重要的高點時間窗，在6月初應該很小心了。
拓展可公度性原理及其誤差糾正
根據可公度性的原理，按照公曆日計算，以1990年12月為起點0，平均每隔9個月左右就出現一個重要轉折點。如下表
| 時間跨度 | 年份月份 | 與轉折點的誤差 | 時間跨度 | 年份月份 | 與轉折點的誤差 |
| 0 | 1990.12 | 上交所開市 | 81 | 1997.9 | 高點 |
| 9 | 1991.9 | 無轉折點 | 90 | 1998.6 | 高點 |
| 18 | 1992.6 | （-1）為高點 | 99 | 1999.3 | （+1）為高點 |
| 27 | 1993.3 | （-1）為高點 | 108 | 1999.12 | 低點 |
| 36 | 1993.12 | 高點 | 117 | 2000.9 | （-1）為高點 |
| 45 | 1994.9 | 高點 | 126 | 2001.6 | 高點 |
| 54 | 1995.6 | （-1）為高點 | 135 | 2002.3 | 高點 |
| 63 | 1996.3 | 低點 | 144 | 2002.12 | （+1）為低點 |
| 72 | 1996.12 | 高點 | 153 | 2003.9 | （+1）為低點 |
| 160 | 2004.4 | （-1）高點 |
這些轉折點幾乎都是高點，同樣可以推斷出今年6月份左右成為高點或者次高點的機率很高。
注意的幾點
任何預測都會存在誤差，可公度性同樣也不例外，如何迴避錯誤、減少誤差，使它成為嚴謹的、科學的、穩定的、有效的預測方法，筆者總結出以下幾點：
1、必須注意數據的分布密度，分布密度有兩重含義
1）同系列數據內部的比較，象去年高點中六、七月份的密度明顯比三月份的高，前者數據為2個121、3個122，後者數據為2個117、2個118、1個119，雖然兩者都是五組數據，但前者只與兩個數有關，所以更重要一些，六、七月份之後基本上就沒有大的反彈。
2）不同系列（高、低點）數據之間的比較，象去年12月份的高點數據組非常多，包括X1+X20=126，X2+X19=125，X4+X18=126，X5+X16=126，X7+X15=126，X8+X13=127，X9+X12=126，X11+X11=126，低點數據組偏少。所以，雖然指數已經大幅下跌了不少，但是反彈後仍然繼續創新低。
2、必須充分運用反證，高、低點數據有時會有衝突，出現重疊。這時無論是高點還是低點的有效性都大打折扣，行情一般會出現大的波動，並不是重要的轉折點，如果高、低點的數據沒有衝突時就要特別關注。
