數學模式論
正文
運用數學方法,即建立一定的有關學習的數學模式,對學習過程進行研究的理論。關於學習過程的數量分析的理論,在美國心理學家C.L.赫爾的著作中已有某些綱領性的敘述。但是,數學模式論則是20世紀50年代初期由美國W.K.埃斯蒂斯等人所創立的。1951年,埃斯蒂斯發表了關於刺激樣本理論的第一篇文章,以後又繼續進行了大量的研究。一般認為,埃斯蒂斯是數學模式論的代表人物。
數學模式論只是用來探討學習的理論結構的一種特殊方法,並非一種新的關於學習的基本原理。具有不同觀點的心理學家均可運用數學的方法來研究他們的理論。
在學習的研究中運用數學方法,可以發現實驗數據之間的豐富聯繫。數學模式既可用來簡潔地表示關於學習過程的資料,又可用來解釋這些資料。因此,在一定的條件下,運用數學模式可以精確地預測學習的進程。例如,我們可以預測對複合刺激物的反應。如果我們以S1表示複合刺激物中的一組要素與反應A1相聯繫;S2與A2相聯繫;S3表示第三組要素,其中,任意的1/2要素與A1聯繫,1/2要素與A2聯繫。這樣,如果考查由S1中的n1要素,S2中的n2要素,S3中的n3要素組成的複合刺激,那么,預期A1反應的比例是
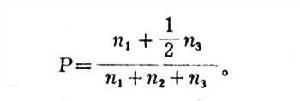
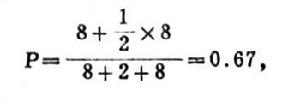
但是,當前所採用的數學模式也有一定的缺陷。現在還沒有一個在任何情況下都能適用的模式。往往是在A情況下所得到的數學模式不適合或不完全適合情況B;而且,現在所得到的模式是雜亂的,不連貫的,缺乏一個全面的聯結系統用以控制眾多類型的模式。
但是,在心理學中運用數學模式已經滲透到許多研究領域之中,所以,在學習的過程中運用數學模式這一潮流還將繼續下去。
參考書目
G.H.Bower, E.R.Hilgard, Theories of learning,Prentice-Hall Press,London,1980.