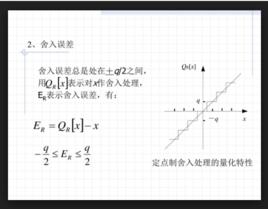
表示誤差
把一個浮點數在計算機中表示,可能會引起誤差,這樣的誤差叫做 表示誤差。例如:
| 數學表達式 | 精確值 | 近似值 | 誤差 |
| 1/7 | 0.142857(OEIS中的數列A020806) | 0.142857 | 0.000000142857 |
| ln 2 | 0.69314718055994530941... (OEIS中的數列A002162) | 0.693147 | 0.00000018055994530941... |
| log2 | 0.30102999566398119521... (OEIS中的數列A007524) | 0.3010 | 0.00002999566398119521... |
| ∛2 | 1.25992104989487316476... (OEIS中的數列A002580) | 1.25992 | 0.00000104989487316476... |
| √2 | 1.41421356237309504880... (OEIS中的數列A002193) | 1.41421 | 0.00000356237309504880... |
| e | 2.71828182845904523536... (OEIS中的數列A001113) | 2.718281828459045 | 0.00000000000000023536... |
| π | 3.14159265358979323846... (OEIS中的數列A000796) | 3.141592653589793 | 0.00000000000000023846... |
增加數字位數可以減少可能會產生的捨入誤差,但是位數是有限的,在表示無限浮點數時仍然會產生誤差。在用常規方法表示浮點數的情況下,這種誤差是不可避免的,但是可以通過設定警戒位來減小。
多步捨入會增加捨入誤差,例如數字9.945309在輸入時被捨入到小數點後兩位 (9.95),顯示時再捨入到小數點後一位 (10.0),捨入誤差是0.054691。如果原來的數隻經過一步捨入到小數點後一位 (9.9),捨入誤差僅為0.045309。
IEEE二進制浮點數算術標準中定義了以下幾種捨入規則:
朝0方向捨入: 即截尾,直接將需要精確的位數以後的數位捨去。
0.142857≈ 0.142 (將小數點後第3位以後的數位全部捨去)
捨入到最接近: 即四捨五入,結果可能會變大或變小。
 捨入誤差
捨入誤差0.142857≈ 0.143 (因小數點後第4位,所以小數點後第3位加1)
 捨入誤差
捨入誤差0.142857≈ 0.14 (因小數點後第3位,所以直接捨去)
朝-∞方向捨入: 總是向數軸的左方向捨入。
朝+∞方向捨入: 總是向數軸的右方向捨入。
舉例
•1990年2月25日,海灣戰爭期間,在沙烏地阿拉伯宰赫蘭的愛國者飛彈防禦系統因浮點數捨入錯誤而失效,該系統的計算機精度僅有24位,存在0.0001%的計時誤差,所以有效時間闕值是20個小時。當系統運行100個小時以後,已經積累了0.3422秒的誤差。這個錯誤導致飛彈系統不斷地自我循環,而不能正確地瞄準目標。結果未能攔截一枚伊拉克飛毛腿飛彈,飛毛腿飛彈在軍營中爆炸,造成28名美國陸軍死亡。
•1996年6月4日,在亞利安五號運載火箭發射後37秒,偏離預定軌道而炸毀。原因是軟體系統試圖將64位浮點數轉換為16位浮點數,造成溢出錯誤。
•溫哥華證券交易所曾開發了一項股票指數。當其在1982年推出時,指數的值是1000.000。在後來的重新計算時多次運用捨入到小數點後三位的操作。22個月以後,指數的值是524.881,然而事實上應該是1009.811。