描述
在大氣科學中研究中，大氣運動方程組是非線性的，直接求解十分困難。常假設某物理量是由其緯向平均值和疊加於其上的小擾動組成，即將非線性方程中的因變數分成不隨時空變化的基本量與隨時空變化的擾動量，基本量是大值而擾動量是小值。將這一假定代入描述大氣運動特徵的非線性微分方程中並假定擾動的乘積項可以略去，則可得到描述小擾動性態的線性微分方程，即擾動方程。這個假設的方法，即為小擾動法。擾動方程除了是線性方程外，還是齊次方程，即方程中每一項或者含有一個因變數，或者含有一個因變數的一階或高階導數，這就使擾動方程容易求解。若假設平均值與經度和時間無關，則擾動方程的解取波動形式。在一定的邊界條件下，可以求得波速與波長以及其他物理量參數的關係 。
擾動方程已經廣泛地用於大氣中聲波、重力波、羅斯貝波、鋒面波等問題的研究中。擾動方程的波動解還可以用於研究大氣運動的穩定性問題。一般的擾動方程都是線性微分方程。
方程
小擾動法的基本做法是 ：
（1）將各物理量看作由兩部分組成，一部分為運動的基本狀態，不隨時間變化；另一部分是波動引起的微擾動部分，表示各變數相對基本狀態的偏差。
（2）基本量滿足原有的方程組和定解條件。
（3）微擾動滿足的方程組和定解條件由原方程組和定解條件減去基本量的方程組和定解條件而得到，且應略去微擾量的二階項。
例如，對大氣運動進行如下假設 ：
將風場分為基本量和擾動量（）,其中，平均緯向風恆定（為常數），平均經向風為0（=0），且沒有平均垂直運動（=0），平均氣壓在南北和垂直方向分布不均勻（），平均密度在垂直方向分布不均勻，並且。則可將大氣運動方程組進行線性化
原方程組
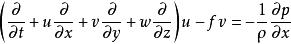擾動方程
擾動方程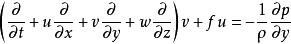
擾動方程
擾動方程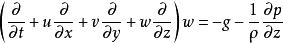
擾動方程
擾動方程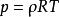擾動方程組
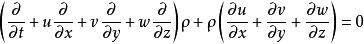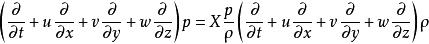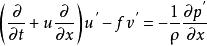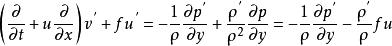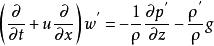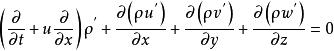擾動方程
擾動方程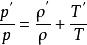
擾動方程
擾動方程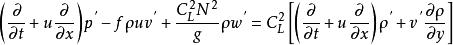
擾動方程
擾動方程擾動方程為線性方程，可求得解析解。
