定義
Gross–Pitaevskii 方程(以Eugene P. Gross命名 與Lev Petrovich Pitaevskii) 描述了全同玻色子量子體系的基態,其中使用了Hartree-Fock近似與贗勢相互作用模型。
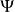 Gross-Pitaevskii方程
Gross-Pitaevskii方程在Hartree-Fock近似中,N個玻色子體系的總波函式為單粒子波函式之積
 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中為第i個玻色子的坐標。
贗勢模型下的哈密頓量為
 Gross-Pitaevskii方程
Gross-Pitaevskii方程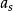 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中m為玻色子質量,V為外勢場,為玻色子-玻色子散射長度,為狄拉克δ函式。
如果單粒子波函式滿足Gross-Pitaevski方程,
 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程則總波函式在歸一化條件下可以使贗勢模型哈密頓量的總能量最小。
Gross-Pitaevski方程是描述玻色-愛因斯坦凝聚單粒子波函式的模型方程。它有類似金茲堡-朗道方程的形式,也會被稱為非線性薛丁格方程.
玻色-愛因斯坦凝聚(BEC) 是處於同一量子態的玻色氣體可以由同一個波函式進行描述。單個粒子可有單粒子波函式描述。真實氣體中粒子相互作用包含在相應的多體薛丁格方程當中。當氣體中粒子間距大於散射長度(即所謂的稀薄極限)時,真實的相互作用勢就可以被替換為贗勢。Gross-Pitaevskii方程的非線性來源於粒子間的相互作用。當把方程中相互作用的耦合常數設為零時,非線性消失,方程以描述單粒子在勢阱中的單粒子薛丁格方程的形式出現。
方程形式
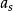 Gross-Pitaevskii方程
Gross-Pitaevskii方程Gross-Pitaevskii方程的形式類似於一般薛丁格方程,但是多出一個相互作用項。耦合常數{\displaystyle g}正比於兩個相互作用玻色子間的散射長度
 Gross-Pitaevskii方程
Gross-Pitaevskii方程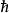 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中為約化普朗克常數。能量密度為
 Gross-Pitaevskii方程
Gross-Pitaevskii方程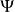 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中為波函式,V為外部勢場。 對於體系內粒子數守恆的不含時Gross–Pitaevskii方程
 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中為化學勢。化學勢是從粒子數與波函式間的關係中得到的
 Gross-Pitaevskii方程
Gross-Pitaevskii方程從不含時Gross-Pitaevskii方程中,我們可以求得各種外勢場中玻色愛因斯坦凝聚的內部結構(例如,諧振子勢阱)。
含時Gross-Pitaevskii方程為
 Gross-Pitaevskii方程
Gross-Pitaevskii方程利用含時Gross–Pitaevskii方程人們可以研究玻色愛因斯坦凝聚的動力學問題。
方程解
鑒於Gross–Pitaevskii方程為非線性偏微分方程,一般很難求得解析解,大多數求解套用近似方法。
精確解
(1)自由粒子
 Gross-Pitaevskii方程
Gross-Pitaevskii方程最簡單的情況是描述自由粒子,外勢場,
 Gross-Pitaevskii方程
Gross-Pitaevskii方程該解常被稱為Hartree解。儘管它滿足Gross–Pitaevskii方程,由於相互作用,其能譜中含有間隙
 Gross-Pitaevskii方程
Gross-Pitaevskii方程根據Hugenholtz–Pines定理, 含斥力相互作用的玻色氣體並無能量間隙。
(2)孤子
一維孤子可以構成玻色愛因斯坦凝聚,取決於相互作用是引力還是斥力,形成亮孤子或暗孤子。兩種孤子都是均勻密度背景下的定域擾動。如若相互作用是斥力形式的, g>0,Gross–Pitaevskii方程的可能解為,
 Gross-Pitaevskii方程
Gross-Pitaevskii方程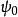 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程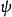 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中為凝聚態波函式在無窮遠處的值,為相干長度。此解代表暗孤子,它描述在空間上原本均勻分布的密度出現了缺失。暗孤子是一種拓撲缺陷,因為在經過原點處符號發生翻轉。這對應了數學上的相移。
對於g<0
 Gross-Pitaevskii方程
Gross-Pitaevskii方程 Gross-Pitaevskii方程
Gross-Pitaevskii方程其中化學勢為。此解為亮孤子, 代表了空間上的凝聚。
變分解
對於難以得到精確解析解的體系,人們可以使用變分法。代入含某可調參數的已知波函式,求解體系自由能,找到使體系能量降為最低的參數。
托馬斯-費米近似
如果氣體中粒子數量很多,原子間相互作用極大,以至於原子自身動能可以從Gross-Pitaevskii方程中忽略,此時近似為托馬斯-費米近似。
 Gross-Pitaevskii方程
Gross-Pitaevskii方程
