定理
 拉比判別法
拉比判別法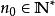 拉比判別法
拉比判別法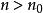 拉比判別法
拉比判別法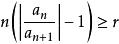 拉比判別法
拉比判別法 拉比判別法
拉比判別法對任意級數 。如果存在r>1,,使得當時,有,那么級數絕對收斂。
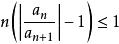 拉比判別法
拉比判別法 拉比判別法
拉比判別法如果對充分大的 n,有,那么級數發散。
極限形式
 拉比判別法
拉比判別法對任意級數 ,令
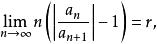 拉比判別法
拉比判別法r>1 時級數絕對收斂;r<1 時級數發散;r=1 時級數可能收斂也可能發散。
證明
當r>1 時,存在p使得 r>p>1,則:
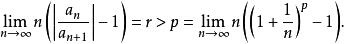 拉比判別法
拉比判別法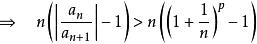 拉比判別法
拉比判別法(對充分大的n)
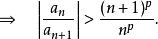 拉比判別法
拉比判別法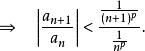 拉比判別法
拉比判別法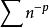 拉比判別法
拉比判別法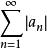 拉比判別法
拉比判別法 拉比判別法
拉比判別法因為當 p>1 時級數收斂,故級數在 r>1時收斂,即級數絕對收斂。
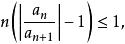 拉比判別法
拉比判別法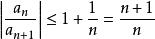 拉比判別法
拉比判別法當 r<1時,有,則,即
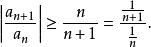 拉比判別法
拉比判別法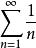 拉比判別法
拉比判別法 拉比判別法
拉比判別法由於 發散,故 發散。
例子
當r=1 時無法判斷其斂散性,舉例如下:
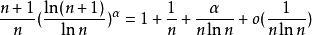 拉比判別法
拉比判別法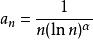 拉比判別法
拉比判別法已知有。令
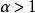 拉比判別法
拉比判別法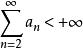 拉比判別法
拉比判別法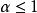 拉比判別法
拉比判別法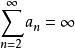 拉比判別法
拉比判別法已知當時,;當時,,然而由上式得
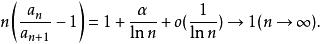 拉比判別法
拉比判別法這說明當r=1時,拉比判別法無效。
