定律定義
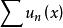 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法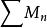 維爾斯特拉斯判別法
維爾斯特拉斯判別法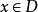 維爾斯特拉斯判別法
維爾斯特拉斯判別法設函式項級數 定義在數集 上, 為收斂的正項級數,若對一切 ,
 維爾斯特拉斯判別法
維爾斯特拉斯判別法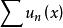 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法則函式項級數數 在 上一致收斂 .
推導過程
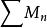 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法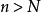 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法由假設正項級數 收斂,根據數項級數的柯西準則,任給正數 ,存在某正整數 ,使得當 及任何正整數 ,有
 維爾斯特拉斯判別法
維爾斯特拉斯判別法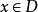 維爾斯特拉斯判別法
維爾斯特拉斯判別法又由(1)式對一切 有
 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法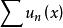 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法根據函式項級數一致收斂的柯西準則,級數 在 上一致收斂.
套用領域
例題
函式項級數
 維爾斯特拉斯判別法
維爾斯特拉斯判別法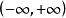 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法在 上一致收斂. 因為對一切 有
 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法而正項級數 是收斂的.
 維爾斯特拉斯判別法
維爾斯特拉斯判別法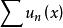 維爾斯特拉斯判別法
維爾斯特拉斯判別法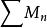 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法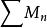 維爾斯特拉斯判別法
維爾斯特拉斯判別法 維爾斯特拉斯判別法
維爾斯特拉斯判別法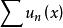 維爾斯特拉斯判別法
維爾斯特拉斯判別法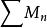 維爾斯特拉斯判別法
維爾斯特拉斯判別法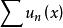 維爾斯特拉斯判別法
維爾斯特拉斯判別法魏爾斯特拉斯定理也稱為 判別法或優級數判別法. 當級數 與級數 在區間 上成立關係式(1)時,則稱級數 在 上優於級數 ,或稱 為級數 的優級數.
