簡介
拉格朗日點(Lagrangian points ) 指在兩大物體引力作用下，能使小物體穩定的點，於1772年由法國數學家拉格朗日推算得出。1906年首次發現運動於木星軌道上的小行星（脫羅央群小行星）在木星和太陽的作用下處於拉格朗日點上。
在每個由兩大天體構成的系統中，按推論有5個拉格朗日點，但只有兩個是穩定的，即小物體在該點處即使受外界引力的攝擾，仍然有保持在原來位置處的傾向。每個穩定點同兩大物體所在的點構成一個等邊三角。
發現
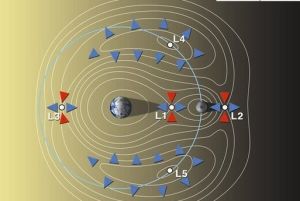地月拉格朗日點示意圖18世紀法國數學家、力學家和天文學家拉格朗日在1772年發表的論文“三體問題”中，為了求得三體問題的通解，他用了一個非常特殊的例子作為問題的結果，即：如果某一時刻，三個運動物體恰恰處於等邊三角形的三個頂點，那么給定初速度，它們將始終保持等邊三角形隊形運動。
1906年，天文學家發現了第588號小行星和太陽正好等距離，它同木星幾乎在同一軌道上超前60°運動，它們一起構成運動著的等邊三角形。同年發現的第617號小行星也在木星軌道上落後60°左右，構成第2個拉格朗日正三角形。
20世紀80年代，天文學家發現土星和它的大衛星構成的運動系統中也有類似的正三角形。人們進一步發現，在自然界各種運動系統中，都有拉格朗日點。
原理
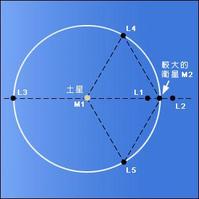拉格朗日點由於拉格朗日點的作用不僅體現在巨觀世界，也體現在微觀世界，因此人們認識到凡是沒有拉格朗日點構成的物質都是不穩定的。拉格朗日發現這種奇異點在天體運動系統中有5個，用字母L表示。L1、L2和L3在兩個天體的聯線上，為不穩定點。如一個物體在這些點上稍微挪動一下，就會離去，不再復位。L4、L5是穩定點。一個物體在此點上稍有移動，不會脫離，而是繞這個點作往返擺動，為此，它又稱作拉格朗日平動點。
事例
拉格朗日點存在於雙星系統、行星和太陽、衛星和行星 (或任何因重力牽引而相互繞行的兩個天體) 的軌道面上。
例如，超前和落後木星軌道60度的地方，各有一個拉格朗日點，如果有小行星在這兩個拉格朗日點上，它會在此點附近振盪，但不會離開這些點，而特洛伊小行星 (Trojan asteroids) 就是位在這兩個區域。而任何“雙星系統”都有五個拉格朗日點。除了上面的兩個點之外，另三個的拉格朗日點不很穩定，位在其他拉格朗日點上的小天體，稍受擾動就會離開它位置。
5個點
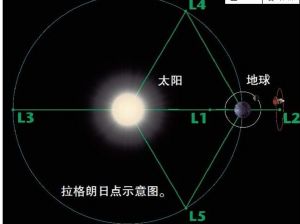
L1
拉格朗日點示意圖在M1和M2兩個大天體的連線上，且在它們之間。
例如：一個圍繞太陽鏇轉的物體，它距太陽的距離越近，它的軌道周期就越短。但是這忽略了地球的萬有引力對其產生的拉力的影響。如果這個物體在地球與太陽之間，地球引力的影響會減弱太陽對這物體的拉力，因此增加了這個物體的軌道周期。物體距地球越近，這種影響就越大。在L1點，物體的軌道周期恰好等於地球的軌道周期。太陽及日光層探測儀即圍繞日-地系統的L1點運行。
L2
在兩個大天體的連線上，且在較小的天體一側。
例如：相似的影響發生在地球的另一側。一個物體距太陽的距離越遠，它的軌道周期通常就越長。地球引力對其的拉力減小了物體的軌道周期。在L2點，軌道周期變得與地球的相等。 L2通常用於放置空間天文台。因為L2的物體可以保持背向太陽和地球的方位，易於保護和校準。威爾金森微波異性探測器就是圍繞日-地系統的L2點運行。詹姆斯·韋伯太空望遠鏡被放置在日-地系統的L2點上。
L3
在兩個大天體的連線上，且在較大的天體一側。
例如：第三個拉格朗日點，L3，位於太陽的另一側，比地球距太陽略微遠一些。地球與太陽的合拉力再次使物體的運行軌道周期與地球相等。 一些科幻小說和漫畫經常會在L3點描述出一個“反地球” 。
L4
在以兩天體連線為底的等邊三角形的第三個頂點上，且在較小天體圍繞較大天體運行軌道的前方。
L5
在以兩天體連線為底的等邊三角形的第三個頂點上，且在較小天體圍繞較大天體運行軌道的後方。
L4和L5有時稱為“三角拉格朗日點”或“特洛伊點”。土衛三的L4和L5點有兩個小衛星，土衛十三和土衛十四。土衛四在L4點有一個衛星土衛十二。
用途
在天體力學中，拉格朗日點是限制性三體問題的5個特解。例如，兩個天體環繞運行，在空間中有5個位置可以放入第三個物體（質量忽略不計），並使其保持在兩個天體的相應位置上。理想狀態下，兩個同軌道物體以相同的周期鏇轉，兩個天體的萬有引力提供在拉格朗日點需要的向心力，使得第三個物體與前兩個物體相對靜止。
理性在太空閃光按照計畫，美國國家航空航天局要對哈勃空間望遠鏡（HST）進行第5次維修。維修之後，人們估計它至少能夠再工作5年。HST一時還不“退休”，“繼任者”詹姆斯·韋伯空間望遠鏡（JWST）只好在地面上再靜候幾年了。
有趣的是，詹姆斯·韋伯空間望遠鏡將不像HST那樣繞著地球公轉，它的“工作地點”被定在太陽-地球系統的“第二拉格朗日點”（在地球背向太陽一面的150萬千米處）。拉格朗日（1736—1813）怎么也想不到，他的“三體問題”研究成果，在發表200多年之後，屢次在人類的科學研究與航天工程中被引用。
在雙星系統、行星和太陽、衛星和行星(或任何因重力牽引而相互繞行的兩個天體)的軌道面上，所特有的一些穩定點。例如，超前和落後木星軌道60度的地方，各有一個拉格朗日點，如果有小行星在這兩個拉格朗日點上，它會在此點附近振盪，但不會離開這些點，而特洛伊小行星(Trojanasteroids)就是位在這兩個區域。事實上，任何「雙星系統」都有五個拉格朗日點。除了上面的兩個點之外，另三個的拉格朗日點不很穩定，位在其他拉格朗日點上的小天體，稍受擾動就會離開它位置。
“三體問題”研究成果被後人使用，JWST不是第一例。更早受到世界矚目的是2001年升空的威爾金森宇宙微波各向異性探測衛星（WMAP），WMAP是繼宇宙微波背景探索者衛星COBE之後的第二代宇宙微波背景探測衛星。人們感到好奇的，也是WMAP的定位：處於太陽-地球系統的“第二拉格朗日點”。
讓我們說一說，什麼是“三體問題”？簡單地說，就是“太陽-地球-小質量物體”，或者“太陽-木星—小質量物體”這樣的“三個天體”的系統如何運行。說得詳細一點，就是研究這樣的問題：“太陽-地球”或者“太陽-木星”這些天體系統，如果有無限小質量的物體加入進來，那么在萬有引力作用下，這些小物體會怎樣運動？
“三體問題中”最簡單的一種類型，是“平面圓形限制三體問題”。拉格朗日求解這個問題，得到了5個特解：3個直線解和兩個等邊三角形解,只有兩個等邊三角形解是穩定解。如果小質量物體處在某一個拉格朗日點上，那么它所受到的太陽-木星（或太陽-地球）的引力，恰好等於它與太陽-木星（或太陽-地球）一起轉動時所需要的向心力。這就是說，處在某一個拉格朗日點上，小質量物體就可與太陽-木星（或太陽-地球）的相對位置保持不變。
有趣的是，“第一代衛星”HST和COBE都是繞著地球“公轉”，“第二代衛星”JWST和WMAP都把位置定在太陽-地球系統的“第二拉格朗日點”。歐洲空間局的兩顆衛星“赫歇爾”、“GAIA”也看好那個“地點”，計畫到那裡落戶。
在科學發展的歷史上，跟“三體問題”有關的好玩故事還有不少。大約一百年前，1906年，德國天文學家馬克思·沃爾夫發現了一顆奇異的小行星。它的軌道與木星相同，而不在通常所說火星軌道與木星軌道之間的小行星帶里。最奇妙的是，它的繞日運動周期與木星相同。從太陽看去，它總是在木星之前60°運轉，不會與木星貼近。這顆小行星被命名為“阿基里斯”，他是荷馬史詩《伊里亞特》敘述的特洛伊戰爭中的希臘英雄。
天文學家沙利葉敏感地意識到，小行星“阿基里斯”很可能是法國數學家拉格朗日“三體問題”的一個特例：只要小物體、大行星與太陽這三者形成一個等邊三角形，這小物體和大行星就會永遠同步地繞太陽鏇轉，它們永遠不會相撞。
果然，天文學家很快就在木星之後60°的位置上，也發現了小行星。迄今為止，在木星前後這兩個拉格朗日點上，已找到700顆小行星。科學理論的預見何其美妙！後來發現的這些處在拉格朗日點上的小行星，都以特洛伊戰爭里的英雄命名。於是，這幾百顆小行星，就有了一個“集體的”稱號：特羅央群小行星。這個“特羅央”，實際上就是古希臘神話中小亞細亞的“特洛伊”城。
不久前，法國空間研究中心的天文學家提出一個新構想，使得拉格朗日點將來可能獲得新的用途：用作攔截危險小行星的布防點。法國科學家提出，捕獲一些中等體積的“天體”，把它們“部署”到“太陽—地球”體系的五個拉格朗日點中的一個。發現對地球有危險的小行星以後，人們可以調用這些“天體”去攔截危險小行星。
美妙的理論、美麗的圖像、美好的套用，拉格朗日帶給我們的興趣是全方位的：理趣、情趣、志趣。這是我們對科學的全面的美感。
相關事件
NASA月球空間站定點在地月拉格朗日點
2012年11月20日，據國外媒體報導，美國宇航局計畫在地球和月球的拉格朗日點上建設空間站。地月拉格朗日點處於地球和月球連線的延長線上，距離月球65000公里。由於處於該點的太空飛行器還要受到太陽引力的干擾，實際運行軌跡非常複雜，形成了圍繞地-月L2的暈軌道。處於地月拉格朗日點上的空間站能夠為太空人和工程師積累深空操作的經驗，最終會確保人類脫離地月系統而探索更為廣闊的宇宙空間。地月拉格朗日點上的空間站還能夠作為維修大型天文望遠鏡的平台，並且由於地月拉格朗日點距離月球較近，因此還可以用來對月球上的地質勘探機器人進行實時遙控。
