基本介紹
拉格朗日鞍點(Lagrange saddle point)是非線性規劃問題中滿足特定條件的點。對於非線性規劃問題(NP)(參見下文“非線性規劃”)，它的拉格朗日函式是指目標函式和約束條件中函式的如下線性組合：
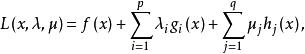拉格朗日鞍點
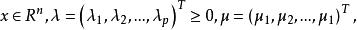拉格朗日鞍點其中滿足條件
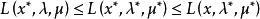拉格朗日鞍點
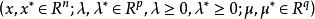拉格朗日鞍點
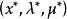拉格朗日鞍點的點稱為(NP)的 拉格朗日鞍點。
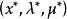拉格朗日鞍點 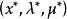拉格朗日鞍點
拉格朗日鞍點定理 設是凸最佳化問題的KKT點，則為對應的拉格朗日函式的鞍點，同時也是該凸最佳化問題的全局極小點 。
鞍點定理
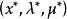拉格朗日鞍點 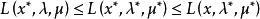拉格朗日鞍點 拉格朗日鞍點鞍點定理(saddle point theorem)是關於拉格朗日函式的鞍點與約束最佳化問題最優點之間的關係定理。鞍點是函式平穩點的一種，套用鞍點的性質，可以推得最優點的充分條件如下：對於約束極小化問題，如果其拉格朗日函式的鞍點存在，即有，那么相應的必是該約束極小化問題的最優點。由於沒有涉及函式的凸性與可微性，適用範圍較廣，但因求解鞍點很困難， 且即使原問題的最優點存在，它的拉格朗日函式也不一定有鞍點，故目前並不實用 。
相關概念
非線性規劃
非線性規劃(nonlinear programming)是數學規劃的一個重要分支，它研究目標函式或約束條件中的函式有一個或多個是變數的非線性函式的數學規劃問題。其研究的問題，稱為 非線性規劃問題，簡稱 非線性規劃，記為( NP)。極小化形式的非線性規劃問題的數學模型為
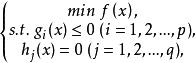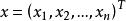拉格朗日鞍點
拉格朗日鞍點
拉格朗日鞍點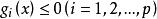
拉格朗日鞍點
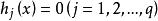拉格朗日鞍點
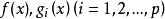拉格朗日鞍點
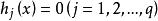拉格朗日鞍點 拉格朗日鞍點
拉格朗日鞍點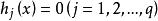 拉格朗日鞍點
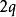拉格朗日鞍點其中是n維歐氏空間中的向量，是目標函式，和是約束條件，並且在和中至少有一個是的非線性函式，因q個等式約束可以化成與它等價的個不等式約束
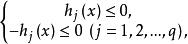拉格朗日鞍點
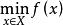拉格朗日鞍點
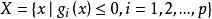拉格朗日鞍點故非線性規劃的數學模型可寫成另一形式，其中。
拉格朗日法
拉格朗日法(Lagrange method)是利用拉格朗日函式，把約束非線性規劃問題轉化為無約束極小化問題求解的一種方法。對於非線性規劃問題
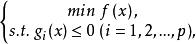拉格朗日鞍點 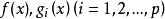拉格朗日鞍點設均具有一階連續偏導數，將拉格朗日函式表示為上述非線性規劃問題的目標函式與加權約束函式之和：
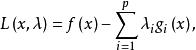拉格朗日鞍點
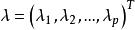拉格朗日鞍點其中是拉格朗日乘子。令其各偏導數為零，得到一方程組，解此方程組可得到非線性規劃問題的最優解 。
