勞思方程
正文
一個動力學方程。是E.J.勞思於1876年提出的。他利用廣義動量積分(見拉格朗日方程)把拉格朗日方程降階,得到了仍舊保持拉格朗日方程形式的動力學方程。一個有N個自由度的保守系統,它有N個廣義坐標qi(i=1,2,…,N)。但在這個系統的拉格朗日函式(見拉格朗日方程)L中, 並不包含某些坐標,設為q1,q2,…,qk(k<N),這些坐標稱為循環坐標。對應於循環坐標有廣義動量積分
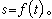
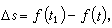

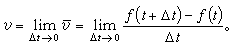
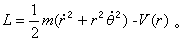 式中L不含Θ,所以Θ是循環坐標。循環積分為
式中L不含Θ,所以Θ是循環坐標。循環積分為 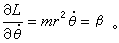 (1)
(1)
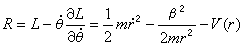 代入勞思方程
代入勞思方程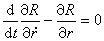 ,得
,得 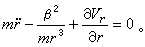 (2)
(2)
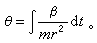
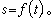
一個動力學方程。是E.J.勞思於1876年提出的
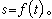
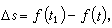

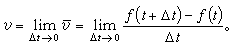
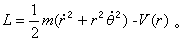 式中L不含Θ,所以Θ是循環坐標。循環積分為
式中L不含Θ,所以Θ是循環坐標。循環積分為 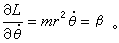 (1)
(1)
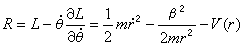 代入勞思方程
代入勞思方程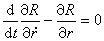 ,得
,得 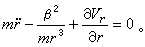 (2)
(2)
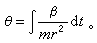
《上帝擲骰子嗎》 摘要 愛因斯坦:「一個人的價值,應該看他貢獻了什麼,而不是他取得了什麼。」 愛因斯坦說:「我不相信上帝是靠擲骰...
《上帝擲骰子嗎》 序 第一章 黃金時代 第二章 烏雲 第三章 火流星等式的證明,方程思想指路明。 萬能公式不一般,化為有理式居先。公式順用...的方程,化為最簡求解集; 《不等式》 解不等式的途徑,利用函式的性質...項和。兩個有限求極限,四則運算順序換。 數列問題多變幻,方程化歸整體...
簡介 公式口訣 必修1 必修2 必修3: 勞思表格法設給定代數方程Pn(x)=0的係數都是實數,其中α0=1。勞思表格的計算方法如下: 其他行的數的計算公式為利用勞思表格可以對根的位置作出判斷。如果勞思表格上最左列自上而下n+1個數均為正數,則虛軸...
簡介 劈因子法 伯努利法 勞思表格法 參考書目力學史力學史力學史,是力學的一個分支,也是科學史的一個分支,它記述和研究人類從自然現象和生產活動中認識和套用物體機械運動規律的歷...
力學史 古代的力學 中世紀的力學 經典力學 力學主要分支工程科學問題的物理和力學摸型,數學方程,計算方法, 計算公式, 程式設計...局部微分正反算法 (SGILD)求解Schordinger薛定格方程。具複雜勢能的三維Schordinger薛定格方程的理論解或漸近理論解方法都...
簡介 工作和學習詳細簡歷,提出海倫公式。 一世紀左右,古希臘的梅內勞發表《球學》,其中包括球...方程求正根的問題。 628年,印度的婆羅摩笈多研究了定方程和不定方程、四邊形、圓周率、梯形和序列。給出了方程ax+by=c(a,b,c是整數...
他轉學到瑞士阿勞市的州立中學。1896年進蘇黎世工業大學師範系學習物理學...著名的物理學家韋伯教授的建議,在瑞士阿勞市的州立中學念完中學課程,以取得...
基本資料 個人概述 職業生涯 個人榮譽 著作概述福建莆田學院醫學部綜合大樓中文:莆田學院英文:Putian University莆田學院(Putian University...
概述 建校歷史 學校現狀 學院規劃 辦學條件率係數,且用這兩個係數結合美軍的兵力增補率構成一個特殊的蘭切斯特方程。它...8求出戰鬥人數遞歸方程的解有一個好處,當交火次數在1到n之間取值時,即可通過遞歸方程的解求出每一輪過後兩隊的剩餘人數。 蘭切斯特第二法則...
系統思考摘要 控制理論的系統思考模型 系統思考在戰爭、管理學和經濟學套用概述