拉格朗日方程

拉格朗日方程，英文名：lagrange’s equations，因約瑟夫·路易斯·拉格朗日而命名，是拉格朗日力學的主要方程，可以用來描述物體的運動，特別適用於理論物理的研究。拉格朗日方程的功能相等於牛頓力學中的牛頓第二定律。

基本信息

• 中文名：拉格朗日方程
• 英文名：lagrange’s equations

• 別名：歐拉-拉格朗日方程
• 優點：廣義坐標個數通常比x坐標少等

簡介

拉格朗日方程：對於完整系統用廣義坐標表示的動力方程，通常系指第二類拉格朗日方程,是法國數學家J.-L.拉格朗日首先導出的。

通常可寫成：

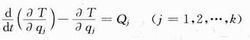
式中T為系統用各廣義坐標qj和各廣義速度q'j所表示的動能；Qj為對應於qj的廣義力;N(=3n-k)為這完整系統的自由度；n為系統的質點數；k為完整約束方程個數。

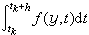
從虛位移原理可以得到受理想約束的質點系不含約束力的平衡方程，而動靜法(達朗貝爾原理)則將列寫平衡方程的靜力學方法套用於建立質點系的動力學方程，將這兩者結合起來，便可得到不含約束力的質點系動力學方程,這就是動力學普遍方程。而拉格朗日方程則是動力學普遍方程在廣義坐標下的具體表現形式。

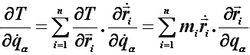
通常，我們將牛頓定律及建立在此基礎上的力學理論稱為牛頓力學(也稱矢量力學)，將拉格朗日方程及建立在此基礎上的理論稱為拉格朗日力學。拉格朗日力學通過位形空間描述力學系統的運動，它適合於研究受約束質點系的運動。拉格朗日力學在解決微幅振動問題和剛體動力學的一些問題的過程中起了重要的作用。拉格朗日方程可以用來建立不含約束力的動力學方程，也可以用來在給定系統運動規律的情況下求解作用在系統上的主動力。如果要想求約束力，可以將拉格朗日方程與動靜法或動量定理(或質心運動定理)聯用。

套用

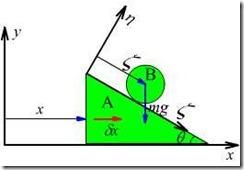拉格朗日方程

用拉格朗日方程解題的優點是：①廣義坐標個數通常比x坐標少，即N<3n，故拉氏方程個數比直角坐標的牛頓方程個數少，即運動微分方程組的階數較低，問題易於求解；②廣義坐標可根據約束條件作適當的選擇，使力學問題的運算簡化，並且不必考慮約束力；③T和L都是標量，比力的矢量關係式更易表達，因此較易列出動力方程。下面是兩個例子：

①圖1是一個半徑為a、質量為m的圓盤，它的中心用鉸鏈與質量為m的直桿相連。此桿的另一端用鉸鏈固接在半徑為b的空心圓筒的中心O；桿長l=b-a。圓盤繞O點擺動。桿的動能為

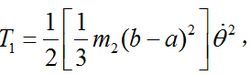
圓盤轉動角關係為bθ=a(θ+φ)，圓盤繞O點轉動動能為

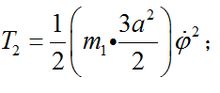
系統以B點為標準的勢能V和系統的動能T為：

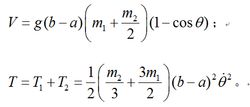
代入

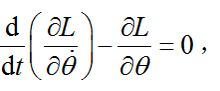
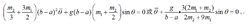
形式

拉格朗日方程

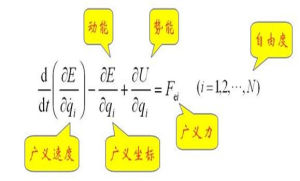拉格朗日方程的一般形式是：式中T為用各廣義坐標qi和廣義速度qi導表示的系統的動能；Qi為對應qi的廣義力。方程式的個數等於系統的自由度N。保守系統中存在勢函式V（q1，q2，…，qN；t)，則廣義力距Q=?V/?qi，又因V中不含qi，即?V/?qi=0，故完整保守系統的拉格朗日方程為：d/dt(?L/?qi)-(?L/?qi)=0（i=1，2，…，N)在非保守體系中，廣義力不能用Q=？V/?qi表示，此時應引入廣義勢能U的概念，Q=?U/?qi-d/dtx?U/(dqi/dt).帶入一般形式可以得到非保守體系的拉格朗日方程。
式中L=T－U為拉格朗日函式，它等於系統的動勢T與位勢U之差。上式與變分問題中的歐拉方程形式相同，由此可導出哈密頓原理。