簡介
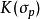 截面曲率
截面曲率 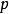 截面曲率
截面曲率 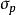 截面曲率
截面曲率 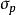 截面曲率
截面曲率 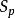 截面曲率
截面曲率 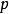 截面曲率
截面曲率 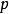 截面曲率
截面曲率 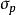 截面曲率
截面曲率 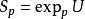 截面曲率
截面曲率 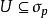 截面曲率
截面曲率 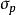 截面曲率
截面曲率 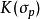 截面曲率
截面曲率 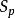 截面曲率
截面曲率 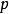 截面曲率
截面曲率 截面曲率 依賴於 點的切空間裡的一個二維平面 。它就定義為該截面,考慮在 p點以平面 作為切平面的曲面 ,這曲面是收集流形中某包含 的鄰域內從 p點出發的測地線且這測地線在 點的切向量屬於截面 (換句話說就是其中 是 里包含原點的鄰域)而截面曲率 就是曲面 在 點的高斯曲率。形式上,截面曲率是流形上的2維格拉斯曼纖維叢的光滑實值函式。
截面曲率完全決定了曲率張量,是非常有用的幾何概念。
定義
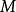 截面曲率
截面曲率 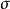 截面曲率
截面曲率 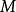 截面曲率
截面曲率 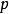 截面曲率
截面曲率  截面曲率
截面曲率  截面曲率
截面曲率 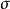 截面曲率
截面曲率 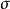 截面曲率
截面曲率 設為黎曼流形, 為上點處切空間中的二維平面,和為中兩個線性無關的向量。 則關於的 截面曲率定義為 :
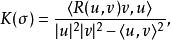 截面曲率
截面曲率 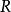 截面曲率
截面曲率 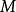 截面曲率
截面曲率 其中是 的黎曼曲率張量。
常截面曲率流形
常截面曲率的黎曼流形是最簡單的類型。它們稱為空間形式。通過縮放度量,它們有三種情況 :
1) 負曲率−1,雙曲幾何;
2) 零曲率,歐幾里得幾何;
3) 正曲率+1,橢圓幾何。
三類幾何的模型流形分別是雙曲空間,歐幾里得空間和單位球面。它們是對於這些給定的截面曲率唯一可能的完備單連通黎曼流形,所有其它常曲率流形是它們在某個等距映射群下的商。
性質
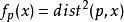 截面曲率
截面曲率 1. 完備黎曼空間有非負的截面曲率,若且唯若函式對於所有點 p是一個1-凹函式。
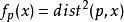 截面曲率
截面曲率 2. 一個完備單連通黎曼流形有非正截面曲率,若且唯若函式是1-凸函式。
相關擴展
• 黎曼曲率張量
• 黎曼流形的曲率
• 曲率
