定義
在廣義相對論中,復曲率是愛因斯坦 - 希爾伯特動作的拉格朗日密度。 該度量下的拉格朗日的歐拉拉格朗日方程構成了真空愛因斯坦場方程,靜態度量被稱為愛因斯坦度量。 n歧管的標量曲率被定義為Ricci張量的軌跡,並且其可以被定義為在某一點處的截面曲率的平均值的n(n-1)倍。
粗略看來,尺度至少為3的標量曲率似乎是一個微不變數,對歧管的全局幾何形狀影響不大,但實際上一些深層定理顯示出標量曲率的力量。 一個這樣的結果是Schoen,Yau和Witten的正質量定理。 相關結果幾乎完全了解哪些歧管具有正標量曲率的黎曼度量。
表示
標量曲率通常由S表示(其他符號為Sc,R)。 它被定義為相對於度量的Ricci曲率張量的軌跡:
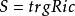 復曲率
復曲率軌跡取決於度量,因為Ricci張量是(0.2)數量張量;必須首先提出一個索引以獲得(1,1)價格張量以便追蹤。在本地坐標方面可以寫
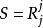 復曲率
復曲率其中Rij是Ricci張量在坐標上的組成部分。
與Riemann曲率張量或Ricci張量不同,兩者都可以用於任何仿射連線,標量曲率需要某種度量。該度量可以是偽黎曼而不是黎曼(Riemannian)。的確,這樣的泛化對於相對論來說至關重要。更一般地說,Ricci張量可以在更廣泛的公制幾何形狀(通過直接幾何解釋,下面)定義,包括Finsler幾何。
直觀幾何表示
當一個點的標量曲率為正時,圍繞該點的小球的體積比歐幾里得空間中具有相同半徑的球的體積更小。另一方面,當一個點的標量曲率為負時,小球的體積大於歐幾里德空間的體積。
這可以被更多地定量化,以便表征黎曼n歧管{\ displaystyle(M,g)}(M,g)的點p處的標量曲率S的精確值。即,給出了在歐幾里得空間中,歧管中半徑ε的n維體積與相應球的n維體積之比,對於小ε,在半徑ε= 0時評估的該比率的二階導數正好減去標量曲率除以3(n + 2)。
這些球的邊界是半徑為的(n-1)維的球體。
