黎曼流形
一黎曼度量的微分流形.設M是n維光滑流形，若在M上給定一個光滑的二階協變張量場g，稱(M，g)為一個n維黎曼流形，g稱為該黎曼流形的基本張量或黎曼度量，如果滿足：
1.g是對稱的，即
g(X，Y)=g(Y，X) (X，Y∈TM，p∈M).
2.g是正定的，即
g(X，X)≥0 (X∈TM，p∈M)，
且等號僅在X=0時成立。
簡單地說，黎曼流形就是給定了一個光滑的對稱、正定的二階張量場的光滑流形。
里奇曲率
里奇曲率是截面曲率的一種平均。設(M，g)是黎曼流形，Ric(·，·)是其里奇張量，對任意的非零切向量X∈TM，若：
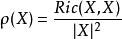數量曲率 則稱ρ(X)為黎曼流形M在切向量X所決定的方向上的里奇曲率。里奇曲率ρ(X)恰好等於包含X在內的各個二維切子空間上的截面曲率(參見“截面曲率”)的平均值.確切地說，若e，e，…，e∈TM是與X正交的n-1個彼此正交的單位切向量，則：
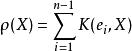數量曲率 其中n=dimM。
曲率張量
由聯絡確定的一個重要張量。設(M，)是仿射聯絡空間，R(X，Y)是曲率運算元，其中X，Y∈Γ(TM).映射X，Y，Z→R(X，Y)Z給出了從Γ(TM)×Γ(TM)×Γ(TM)到Γ(TM)的C(M)線性映射，因此，它在每一點p∈M給出了從TM×TM×TM到TM的多線性映射，即它是一個(1，3)型張量場，稱為(M，)上的曲率張量。在局部坐標系(U;x)下，記：
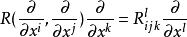數量曲率 R就是曲率張量的分量.由定義得到：
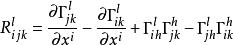數量曲率 其中Γ是聯絡的係數。若(M，g)是黎曼流形，δ是其黎曼聯絡，則能夠定義(M，g)上的4階協變的曲率張量R(X，Y，Z，W)=g(R(X，Y)Z，W)。記：
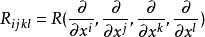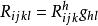數量曲率 
數量曲率 (0，4)型曲率張量有下列性質：
1. R(X，Y，Z，W)=-R(Y，X，Z，W)
=-R(X，Y，W，Z).
2. R(X，Y，Z，W)=R(Z，W，X，Y).
3. R(X，Y，Z，W)+R(X，Z，W，Y)+R(X，W，Y，Z)=0.
數量曲率的概念
數量曲率(scalar curvature)是里奇曲率的平均。設(M，g)是n維黎曼流形，R(·，·，·，·)是其曲率張量，對於TM中的單位正交基{e}，若：
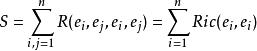數量曲率 則S與單位正交基{e}的選取無關，稱S為M在點p的數量曲率.數量曲率S是在點p的各個切方向上的里奇曲率的平均值，即：
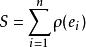數量曲率 若用里奇張量在局部坐標系(U;x)下的分量來表示，則：
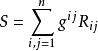數量曲率 意義
在黎曼幾何中，數量曲率（或Ricci標量）是黎曼流形的最簡單的曲率不變數。對於黎曼流形上的每個點，它分配由該點附近的歧管的固有幾何確定的單個實數。具體來說，標量曲率表示在歐氏空間中，黎曼流形中的小測球的體積與標準球的體積的偏差量。在二維上，標量曲率是高斯曲率的兩倍，並且完全表征了曲面的曲率。然而，在兩個維度上，黎曼流形的曲率涉及多個功能獨立的數量。
在廣義相對論中，數量曲率是愛因斯坦 - 希爾伯特動作的拉格朗日密度。在量度變化下，拉格朗日的歐拉 - 拉格朗日方程組成真空愛因斯坦場方程，靜態度量稱為愛因斯坦度量。 n歧管的標量曲率被定義為Ricci張量的軌跡，並且其可以被定義為在某一點處的截面曲率的平均值的n（n-1）倍。
第一眼感覺，尺度至少為3的標量曲率似乎是一個微小的不變數，對歧管的全局幾何形狀幾乎沒有影響，但實際上一些深層定理顯示了數量曲率的力量。一個這樣的結果是Schoen，Yau和Witten的正質量定理。相關結果幾乎完全了解哪些歧管具有正數量曲率的黎曼度量。
