常曲率黎曼空間

常曲率黎曼空間 Riemannian space of constant curvature截面曲率為常數的黎曼流形，它包括了歐氏空間、球面、雙曲空間為其特例。

常曲率黎曼空間

正文

截面曲率為常數的黎曼流形，它包括了歐氏空間、球面、雙曲空間為其特例。在曲面論中,高斯曲率K為常數的曲面局部地為球面(K>0)，平面（K=0）或雙曲平面(K<0)。在高維時高斯曲率的自然推廣為截面曲率(見黎曼幾何學)。如果黎曼流形M上任何點處的任何二維切平面，其相應的截面曲率均為常數K,則稱此黎曼流形為常曲率黎曼空間。又稱常曲率空間。由著名的舒爾定理知道,如果dim M≥3並且M上每處的截面曲率的數值與二維切平面的選取無關，則截面曲率也必與點的選取無關，即它必為常曲率黎曼空間。局部地,常曲率K的n維黎曼流形的黎曼曲率張量可表為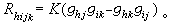此處gij為黎曼流形的度量張量,1≤i，j，k,l≤n。在適當的坐標系下它的黎曼度量為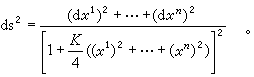

局部地,它是n維球面(K>0)、歐氏空間(K=0)或雙曲空間(K<0)。整體地說,單連通的完備常曲率空間只能是下列三種：球面、歐氏空間和雙曲空間。如不單連通，則其通用覆蓋流形必為上述三類之一。J.A.沃爾夫已完全解決了以球面為其通用覆蓋的緊緻的正常曲率空間的分類。
人們對常曲率黎曼空間感興趣的原因在於這類黎曼流形結構簡單，具有最大的對稱性（即容有最大參數的運動群）,直觀地說,這類空間是均勻各向同性的。它也同時作為共形平坦空間、愛因斯坦空間、齊性黎曼流形或對稱黎曼空間等特殊黎曼流形的一類重要的例子。把它作為模型研究清楚以後，通過與這些標準的模型進行諸如曲率等幾何量的比較，從而可得到對一般黎曼流形的一系列幾何和拓撲的性質。
參考書目
　S.Kobayashi and K.Nomizu,Foundation of Differential Geometry, Vol. 1～2, John Wiley & Sons, New York,1963,1969.
　J.A.Wolf.Spaces of Constant Curvature, McGraw-Hill,New York, 1967.

配圖

相關連線