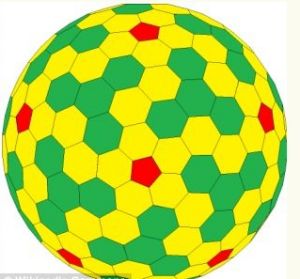
簡介
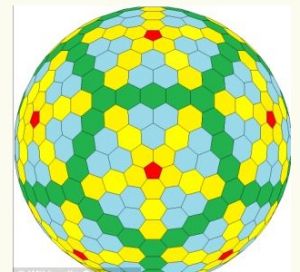科學家400年來首次發現固定“第四類形狀”，稱作“戈德堡多面體”。 美國加利福尼亞大學洛杉磯分校的斯坦·沙因在研究人眼視網膜時偶然發現一種名為格線蛋白的蛋白質具有這種吸引人的多面體結構。該蛋白質負責把能最運入和運出細胞，並創造出眾多的形狀。
沙因對這類形狀提出了一種數學解釋，在這一過程中，他偶然發現了20世紀的數學家麥可·戈德堡的研究成果。戈德堡確信，他發現了一類新形狀，即由五角形和六角形拼起來的複雜多面體。
雖然沙因博士認為，戈德堡的形狀不是嚴格的多面體，但他認為，它們的確是一類新形狀。
沙因和美國數學家詹姆斯·蓋伊德在一份研究報告，描述了這些新形狀。他們仍稱其為戈德堡多面體，向這位已故數學家表達敬意。
分類
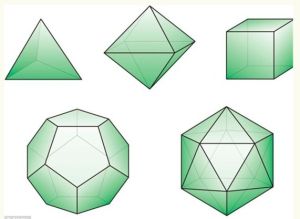第一類固體形狀稱作正多面體，包括立方體、正四面體、正八面體、正十二面體和正二十面體等。 早在幾千年前，古希臘數學家——最引人矚目的是柏拉圖——就對固體形狀進行了分類。自那以後發現的幾何“固體”形狀少之又少，最後一批是在400年前確認的。
科學家發現的第一類固體形狀稱作正多面體，包括立方體、正四面體、正八面體、正十二面體和正二十面體等。
在這些形狀之後又確定了其他兩類固體形狀，即阿基米德多面體（半正多面體）和克卜勒多面體。阿基米德多面體包括截角二十面體。400年前發現的克卜勒多面體包括極其複雜的立體形狀星形正多面體和菱形多面體。
形狀
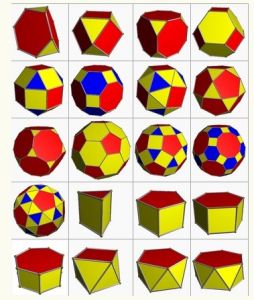阿基米德多面體 英國伯明罕大學數學家戴維·克雷文在評論這項研究成果時，把這些多面體比作像氣球一樣充氣、然後各個面凸起來的多面體。
有爭議的是，原始的戈德堡多面體違反等邊複雜多面體分類的第三條規則，即在把一個形狀上的兩點連線起來的一條線上的任一點一定不在固體形狀之外。
不過，沙因和蓋伊德對這些形狀進行了處理，使它們不再是由多個六角形組成的膨脹形狀。他們發現了一種方法，使這些形狀的所有面都是平的，進而創造出真正的凸多面體。
他們認為，可以將他們處理這些形狀的方法用於其它類的複雜多面體，這樣就會發現擁有越來越多面的更多形狀，從理論上來說，它們的數量應該是無限的。
套用
雖然不研究數學的人可能難以想出這項研究的直接用途，但它令一些科學家興奮，因為這種新多面體的結構類似於病毒。
如果科學家能夠準確描述某種病毒的幾何形狀（比如普通感冒病毒），他們或許就能夠找到更好的方法與這些病毒作鬥爭。
