基本介紹
 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數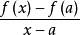 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數設 是定義在區間 上的函式,如果a是區間 內的一點,那么 是定義在區間 內除a以外的 點上的函式,此時如果存在極限:
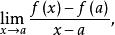 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數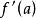 微分係數
微分係數那么就稱 在a點處 可微(differentiable),或者稱在 處 可微,並稱此極限為函式 在a 點處的 微分係數(differentiable coefficient),記為 :
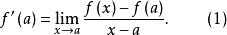 微分係數
微分係數相關概念
可微與導函式
 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數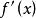 微分係數
微分係數 微分係數
微分係數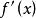 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數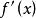 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數當函式 在所屬區間內的任意點x均可微時,則稱函式 可微,或稱函式 關於 x可微。此時 也是定義在區間 上的關於x的函式,稱 為函式 的 導函式(derived function derivative),求函式 的導函式 ,稱為對函式 進行微分,或函式 關於x進行微分。
在(1)式中如果用x替換a,用x+h替換x,則
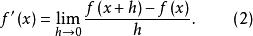 微分係數
微分係數 微分係數
微分係數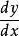 微分係數
微分係數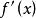 微分係數
微分係數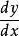 微分係數
微分係數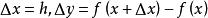 微分係數
微分係數當 時,用 表示 。有時也稱 為 微商(differentiable quotient)。令 ,則
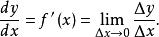 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數定理1如果函式在x點可微,那么函式在x點連續。
推論定義在某區間上的可微函式在該區間上是連續函式。
無窮小量
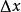 微分係數
微分係數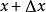 微分係數
微分係數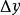 微分係數
微分係數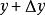 微分係數
微分係數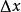 微分係數
微分係數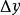 微分係數
微分係數當自變數x增加 成為時,相應地函式y也增加 成為 ,因此把和 分別稱為x和y的 增量(increment)。
 微分係數
微分係數在x點可微時,設
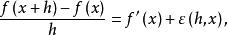 微分係數
微分係數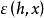 微分係數
微分係數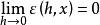 微分係數
微分係數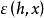 微分係數
微分係數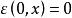 微分係數
微分係數則 是滿足h≠0的h的函式,並且 ,雖然 是定義在h≠0的h的函式,但當h=0時,若定義 ,則對所有的h,
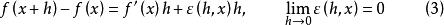 微分係數
微分係數 微分係數
微分係數成立,如果令函式 ,那么
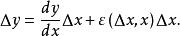 微分係數
微分係數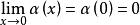 微分係數
微分係數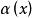 微分係數
微分係數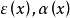 微分係數
微分係數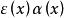 微分係數
微分係數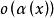 微分係數
微分係數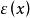 微分係數
微分係數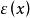 微分係數
微分係數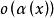 微分係數
微分係數一般地,若 ,則稱函式 為 無窮小量,當 是無窮小量時,無窮小量 用符號 表示,即用小寫字母o來代表 ,在不關心函式 的具體形式時,用符號 很方便。如果使用這個符號,那么上式為:
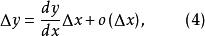 微分係數
微分係數上式(3)可寫為:
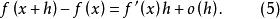 微分係數
微分係數如果用a替換x,用x替換x+h,那么
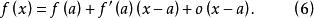 微分係數
微分係數切線
 微分係數
微分係數對在a點處可微的函式 ,把由線性方程式
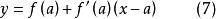 微分係數
微分係數確定的直線:
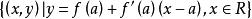 微分係數
微分係數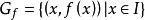 微分係數
微分係數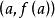 微分係數
微分係數 微分係數
微分係數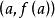 微分係數
微分係數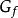 微分係數
微分係數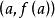 微分係數
微分係數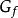 微分係數
微分係數稱為定義在圖像 上 點處函式 的 切線(tangentline)。在高中數學中,也稱它為在 點處圖像 的切線,其方程式是(7),但在我們這裡,把方程式(7)所確定的直線定義為在 點處 的切線。
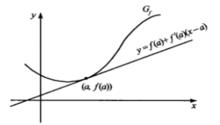 圖1
圖1 微分係數
微分係數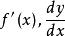 微分係數
微分係數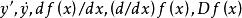 微分係數
微分係數表示函式 的微分係數的符號除 之外,還有 等。
左微分係數和右微分係數
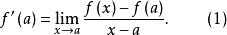 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數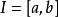 微分係數
微分係數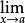 微分係數
微分係數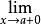 微分係數
微分係數微分係數的定義 中,當a是 的定義域 的左端點,例如 時, 當x從右向a接近時的極限記作 ,所以,
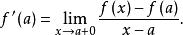 微分係數
微分係數 微分係數
微分係數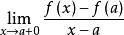 微分係數
微分係數 微分係數
微分係數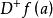 微分係數
微分係數一般地,即使a是 的內點,如果極限 存在,則稱此極限為 在a點處的 右微分係數(right differential coefficient)。用 表示:
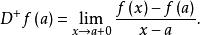 微分係數
微分係數 微分係數
微分係數並且這時,稱 在a點處向右可微,或 右可微(right differentiable)。
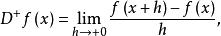 微分係數
微分係數 微分係數
微分係數又,設 ,則
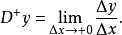 微分係數
微分係數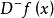 微分係數
微分係數同理可定義左微分係數 。
 微分係數
微分係數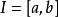 微分係數
微分係數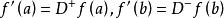 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數 微分係數
微分係數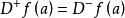 微分係數
微分係數 微分係數
微分係數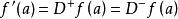 微分係數
微分係數例如,如果 是定義在區間 上的可微函式,則 ,又,如果定義在區間上的函式在的內點a處左可微和右可微,且,那么在a點處可微,並且,。