廣義遞歸論
正文
把自然數集上定義的遞歸論推廣到其他數學結構上去而得到的數學理論。常見的有有窮類型對象上的遞歸論和序數上的遞歸論。有窮類型對象如下定義：自然數稱為0型對象。由n型對象到自然數集的全函式稱為n+1型對象。一型對象φ的計算相當於有一個執行機械過程的機器M，對M輸入數n後可得到輸出m=φ(n)。二型對象F(ƒ,n)的計算相當於上述機器M外加上一個外部信息源即ƒ 的圖形。對輸入ƒ，n,M對輸入n的計算時，常要問機外信息源ƒ對某個變目的值,根據值的不同而依不同的步驟進行計算,最後給出輸出m=F(ƒ,n)。上述兩類計算都是有窮步內完成的計算。三型對象F(F,ƒ,n)的計算相當於上述機器M外加上兩個外部信息源即ƒ的圖形(基數為堗0)和F 的圖形（基數為2
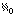）。M對輸入n 的計算時要問到ƒ對某變元的值,和問到F對某變元的值。在問到F對變元g的值時要計算g的圖形,因此此時M的計算不再是有窮步內可停止的計算了。相仿地可有更高類型對象的計算。 還可以把遞歸論推廣到序數上去。最初是用集合論的工具，如降S-L定理,推廣到一切序數上去。後來發展為推廣到序數的某些前節上去。最主要的是推廣到可允許序數上去，稱為α－遞歸論。當α>ω後出現了許多ω-遞歸論中不存在的現象，例如有界和有窮不再是相同的概念了，這就使α-遞歸論的證明大大地複雜了。
ω-遞歸論的某些結果可以推廣到一切可允許序數α上去，例如波斯特問題的解決。有些結果只在某些可允許序數上成立，而在另一些可允許序數上不成立，如極大集的存在性定理。再如當α>ω後，O′以下ω-度的結構和O′以α-度的結構不同構。
