引入
通過考慮這個集合,康托爾和其他數學家奠定了現代點集拓撲學的基礎。雖然康托爾自己用一種一般、抽象的方法定義了這個集合,但是最常見的構造是康托爾三分點集,由去掉一條線段的中間三分之一得出。康托爾自己只附帶介紹了三分點集的構造,作為一個更加一般的想法——一個無處稠密的完備集的例子。
實際上斯梅爾的馬蹄映射也會形成康托爾集。
康托三分集
取一條長度為1的直線段,將它三等分,去掉中間一段,留剩下兩段,再將剩下的兩段再分別三等分,各去掉中間一段,剩下更短的四段,……,將這樣的操作一直繼續下去,直至無窮,由於在不斷分割捨棄過程中,所形成的線段數目越來越多,長度越來越小,在極限的情況下,得到一個離散的點集,稱為康托爾點集,記為P。稱為康托爾點集的極限圖形長度趨於0,線段數目趨於無窮,實際上相當於一個點集。操作n次後
邊長r=(1/3)^n ,
邊數N(r)=2^ ,
根據公式D=lnN(r)/ln(1/r) , D=ln2/ln3=0.631。
所以康托爾點集分數維是0.631。
性質特點
康托三分集中有無窮多個點,所有的點處於非均勻分布狀態。此點集具有自相似性,其局部與整體是相似的,所以是一個分形系統。
康托三分集具有
(1)自相似性;
(2)精細結構;
(3)無窮操作或疊代過程;
(4)傳統幾何學陷入危機。用傳統的幾何學術語難以描述,它既不滿足某些簡單條件如點的軌跡,也不是任何簡單方程的解集。其局部也同樣難於描述。因為每一點附近都有大量被各種不同間隔分開的其它點存在。
(5)長度為零;
(6)簡單與複雜的統一。
康托爾集P具有三條性質:
1、P是完備集。
2、P沒有內點。
3、P的基數為c。
4、P是不可數集。
康托爾集是一個基數為c的疏朗完備集。
三進制理解
在長度為1的直線段中,將所有點按三進制編碼。
即第一次去掉的點,為三進制編碼小數中,第一位小數為1的所有點;同理,第N次操作,就是去掉三進制小數中,第N位為1的點。
最後得到的康托爾集,用三進制表示,就是小數位只有0,2的所有小數。
說明:0.1(3)是康托爾集中的點,但不符合上述描述。在上述描述中,是以0.02(2的循環)表示的。
如果要消除這種循環表示方法,可以定義為:康托爾集,用三進制表示,就是小數位的有效數字最後一位可以為1,2;其他位數只有0,2的所有小數。
構造
康托爾集是由不斷標記線段的中間三分之一而得出。首先,從區間(0,1)中標記中間的三分之一[1/,2/],並選取端點1/、2/,留下兩條線段:(0,1/) ∪ (2/,1)。然後,把這兩條線段的中間三分之一都標記,並選取端點1/、2/、7/、8/,留下四條線段:(0,1/) ∪ (2/,1/) ∪ (2/,7/) ∪ (8/,1)。把這個過程一直進行下去,其中第 n個集合為:
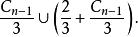 康托爾集
康托爾集康托爾集就是由所有過程中被選取的點組成。

