實質作用
這項定理其實說明了平面向量可以沿任意指定的兩方向分解，同時也說明了由任意兩向量可以合成指定向量，即向量的合成與分解 。當兩個方向相互垂直時，其實就是把他們在直角坐標系中分解，此時（x,y）就稱為此向量的坐標。（此向量的起點為原點）所以此定理為向量的坐標表示提供了理論依據。
坐標表示
在平面直角坐標系中，分別取與x軸，y軸方向相同的兩個單位向量 i、 j作為基底， a為坐標平面內的任意向量，以坐標原點O為起點作向量OP= a。有平面向量基本定理可知，有且只有一對實數x、y，使得
向量OP=x i+y j。
因此向量， a=x i+y j。
我們把實數（x，y）對叫做 向量的坐標，記作： a=（x，y）。
顯然，其中（x，y）就是點P的坐標。
向量OP稱為點P的 位置向量。
共面向量
共面向量基本定理：如果兩個向量 a、 b不共線，那么向量 p與向量 a、 b共面的充要條件是：存在唯一實數對x、y，使 p=x a+y b。
正誤判斷
1．若 a= 0，則對任 a·b≠ 0． 錯（當 a⊥ b時， a · b=0）
2．若 a≠ 0， a · b=0，則 b= 0錯（當 a和 b都不為零，且 a⊥ b時， a · b=0）
3．若 a · b=0，則 a · b中至少有一個為 0. 錯（可以都不為 0，當 a⊥ b時， a · b=0成立）
4．若 a≠ 0， a · b= b · c，則 a= c錯（當 b= 0時）
5．若 a · b= a · c,則 b≠ c,若且唯若 a= 0時成立． 錯（ a≠ 0且同時垂直於 b， c時也成立）
6．對任意向量 a有 a· a=∣ a∣* ∣ a∣
平面向量的線性運算：加法為三角形法則'平行四邊形法則'。定理：向量a與b共線，a不等於零，有且只有唯一一個實數c，使b=ca。
平面向量基本定理
【學習目標】
1．掌握平面向量的基本定理，能用兩個不共線向量表示一個向量；或一個向量分解為兩個向量。
2．能套用平面向量基本定理解決一些幾何問題。
【知識梳理】
若 ， 是不共線向量， 是平面內任一向量
在平面內取一點O，作 = ， = ， = ，使 =λ1 =λ2
= = + =λ1 +λ2
得平面向量基本定理：
注意：1、必須不共線，且它是這一平面內所有向量的一組基底
2、這個定理也叫共面向量定理
3、λ1，λ2是被 ， ， 唯一確定的實數。
例題選講
1．如圖，ABCD是平行四邊形，對角線AC，BD交於M， ， ，試用基底 、 表示 。
2．設 、 是平面內一組基底，如果 =3 -2 ， =4 + ， =8 -9 ，求證：A，B，D三點共線。
3．設是平面內一組基底，如果 =2 +k ， =- -3 ， =2 - ，若A，B，D三點共線，求實數k的值。
4． 中， ，DE//BC，與邊AC相交於點E，中線AM與DE交於點N，如圖， ， ，試用 、 表示 。
歸納反思
1．平面向量基本定理是平面向量坐標表示的基礎，它說明同一平面內的任一向量都可以表示為其他兩個不共線向量的線性組合。
2．在解具體問題時適當地選取基底，使其它向量能夠用基底來表示，選擇了兩個不共線地向量 ，平面內的任何一個向量都可以用 唯一表示，這樣幾何問題就可以轉化為代數問題，轉化為只含 的代數運算。
課內練習
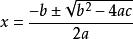平面向量基本定理1．下面三種說法，正確的是
（1）一個平面內只有一對不共線的向量可作為表示該平面所有向量的基底；
（2）一個平面內有無數對不共線的向量可作為表示該平面所有向量的基底；
（3）零向量不可為基底中的向量；
2．如果 、 是平面 內一組基底，，那么下列命題中正確的是
（1）若實數m,n，使m +n = ,則m=n=0;
（2）空間任一向量 可以表示為 = m +n ，這裡m,n是實數；
（3）對實數m,n，向量m +n 不一定在平面 ；
（4）對平面 內的任一向量 ，使 = m +n 的實數m,n有無數組。
3．若G是 的重心，D、E、F分別是AB、BC、CA的中點，則 =
4．如圖，在 中，AM：AB=1：3，AN：AC=1：4，BN與CM交於點P，設 ，試用 ， 表示 。
5．求證：A、B、D三點共線，
