定理
 空間向量
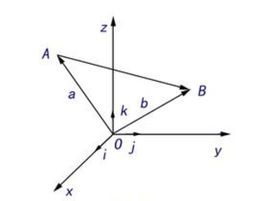
空間向量兩個空間向量a,b向量(b向量不等於0),a∥b的充要條件是存在唯一的實數λ,使a=λb
2、共面向量定理
如果兩個向量a,b不共線,則向量c與向量a,b共面的充要條件是:存在唯一的一對實數x,y,使c=ax+by
3、空間向量分解定理
如果三個向量a、b、c不共面,那么對空間任一向量p,存在一個唯一的有序實數組x,y,z,使p=xa+yb+zc。
任意不共面的三個向量都可作為空間的一個基底,零向量的表示唯一。
卦限
三個坐標面把空間分成八個部分,每個部分叫做一個卦限。含有x軸正半軸、y軸正半軸、z軸正半軸的卦限稱為第一卦限,其他第二、三、四卦限,在xoy面的上方,按逆時針方向確定。在第一、二、三、四卦限下面的部分分別稱為第五、六、七、八卦限。
| 空間向量的八個卦限的符號 | ||||||||
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | |
| x | + | - | - | + | + | - | - | + |
| y | + | + | - | - | + | + | - | - |
| z | + | + | + | + | - | - | - | - |
問題
立體幾何的計算和證明常常涉及到二大問題:一是位置關係,它主要包括線線垂直,線面垂直,線線平行,線面平行;二是度量問題,它主要包括點到線、點到面的距離,線線、線面所成角,面面所成角等。這裡比較多的主要是用向量證明線線、線面垂直及計算線線角,而如何用向量證明線面平行,計算點到平面的距離、線面角及面面角的例題不多,起到一個拋磚引玉的作用。
常識
 空間向量
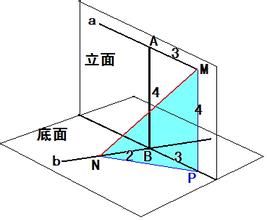
空間向量1、空間一點P位於平面MAB的充要條件是存在唯一的有序實數對x、y,使得PM=xPA+yPB
2、對空間任一點O和不共線的三點A,B,C,若:OP=xOA+yOB+zOC(其中x+y+z=1),則四點P、A、B、C共面.
3、利用向量證a∥b,就是分別在a,b上取向量a=λb(λ∈R).
4、利用向量證a⊥b,就是分別在a,b上取向量a·b=0.
5、利用向量求兩直線a與b的夾角,就是分別在a,b上取a,b,求:<a,b>的問題.
6、利用向量求距離即求向量的模問題.
7、利用坐標法研究線面關係或求角和距離,關鍵是建立正確的空間直角坐標系,正確表達已知點的坐標.
計算
第一步:
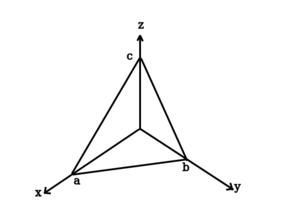
按照圖形建立三維坐標系O-xyz
之後,將點的坐標帶進去,求出所需向量的坐標。
第二步:
求平面的法向量:
令法向量n=(x,y,z)
因為法向量垂直於此平面
所以n垂直於此面內兩相交直線(其方向向量為a,b)
可列出兩個方程n·a=0,n·b=0
兩個方程,三個未知數
然後根據計算方便
取z(或x或y)等於一個數(如:1,√2等)
代入即可求出面的一個法向量n的坐標了.
會求法向量後
1.斜線與平面所成的角就是求出斜線的方向向量與平面的法向量n的夾角,所求角為上述夾角的餘角或者夾角減去π/2.
2.點到平面的距離就是求出該面的法向量n在平面上任取(除被求點在該平面的射影外)一點,
求出平面外那點和你所取的那點所構成的向量,記為a
點到平面的距離就是法向量n與a的數量積的絕對值|n·a|除以法向量的模|n|即得所求.
3.二面角的求法就是求出兩個平面的法向量
可以求出兩個法向量的夾角為兩向量的數量積除以兩向量模的乘積:cos<n,m>=|n·m|/(|n||m|)
那么二面角就是上面求的兩法向量的夾角或者它的補角。
4.設直線l,m的方向向量分別為a,b,平面α,β的法向量分別為μ,ν則
線線平行l∥m<=>a∥b<=>a=kb
線面平行l∥α<=>a⊥μ<=>a·μ=0
面面平行α∥β<=>μ∥ν<=>μ=kν
線線垂直l⊥m<=>a⊥b<=>a·b=0
線面垂直l⊥α<=>a∥μ<=>a=kμ
面面垂直α⊥β<=>μ⊥ν<=>μ·ν=0
5.向量的坐標運算:設a=(x1,y1),b=(x2,y2),則
1.|a|=√(x1²+y1²)
2.a+b=(x1+x2,y1+y2)
3.a-b=(x1-x2,y1-y2)
4.ka=k(x1,y1)=(kx1,ky1)
5.a·b=x1x2+y1y2
6.a∥b<=>x1y2=x2y1(一般寫為:x1y2-x2y1=0)
7.a⊥b<=>a·b=0<=>x1x2+y1y2=0
8.cos<a,b>=(a·b)/(|a|·|b|)=(x1x2+y1y2)/[√(x1²+y1²)·√(x2²+y2²)]
註:x1中的1為下標,以此類推。