定義
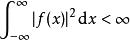 平方可積函式
平方可積函式 平方可積函式
平方可積函式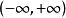 平方可積函式
平方可積函式若 ,則我們說 在實直線 上是平方可積的。平方可積一詞也可以用於有限區間如[0,1] 。
一個等價的定義是,函式本身的平方(而非它的絕對值)是勒貝格可積的。要想使其為真,實部的正和負的部分的積分都必須是有限的,虛部也是如此。
通常這個術語不是指某個特定函式,而是指幾乎處處相等的一組函式。
性質
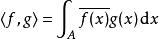 平方可積函式
平方可積函式平方可積函式(這裡的“函式”實際上意味著幾乎處處相等的一組函式)通過內積構成一個內積空間, 其中
 平方可積函式
平方可積函式 平方可積函式
平方可積函式(1) 和 都是平方可積函式;
 平方可積函式
平方可積函式 平方可積函式
平方可積函式(2) 是 的復共軛;
 平方可積函式
平方可積函式 平方可積函式
平方可積函式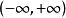 平方可積函式
平方可積函式 平方可積函式
平方可積函式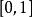 平方可積函式
平方可積函式(3) 是積分區間——在定義的第一種情況中, 就是 ,第二種情況中, 是 。
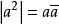 平方可積函式
平方可積函式由於 ,平方可積性之要求也即
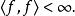 平方可積函式
平方可積函式可以證明,平方可積函式在上述定義的內積導出的度量下構成一個完備度量空間。完備度量空間也被稱柯西空間,因為在這樣的度量空間中,數列收斂若且唯若其為柯西序列。由一個範數導出的度量下的完備空間是巴拿赫空間。因此,平方可積函式的空間是由該範數導出的度量下的巴拿赫空間,而範數又是由內積導出的。由於內積的補充性質,這(空間)其實就是一個希爾伯特空間,因為空間在由內積導出的度量下是完備的。
希爾伯特空間
定義
在數學中,希爾伯特空間是歐幾里德空間的一個推廣,其不再局限於有限維的情形。與歐幾里德空間相仿,希爾伯特空間也是一個內積空間,其上有距離和角的概念(及由此引申而來的正交性與垂直性的概念)。此外,希爾伯特空間還是一個完備的空間,其上所有的柯西序列等價於收斂序列,從而微積分中的大部分概念都可以無障礙地推廣到希爾伯特空間中。希爾伯特空間為基於任意正交繫上的多項式表示的傅立葉級數和傅立葉變換提供了一種有效的表述方式,而這也是泛函分析的核心概念之一。希爾伯特空間是公式化數學和量子力學的關鍵性概念之一。
套用
一個抽象的希爾伯特空間中的元素往往被稱為向量。在實際套用中,它可能代表了一列複數或是一個函式。例如在量子力學中,一個物理系統可以被一個復希爾伯特空間所表示,其中的向量是描述系統可能狀態的波函式。詳細的資料可以參考量子力學的數學描述相關的內容。量子力學中由平面波和束縛態所構成的希爾伯特空間,一般被稱為裝備希爾伯特空間(rigged Hilbert space)。
原理
在一個實向量空間或復向量空間H上的給定的內積 < x,y > 可以按照如下的方式導出一個範數(norm):
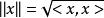 平方可積函式
平方可積函式如果其對於這個範數來說是完備的,此空間稱為是一個希爾伯特空間。這裡的完備性是指,任何一個柯西序列都收斂到此空間中的某個元素,即它們與某個元素的範數差的極限為0。任何一個希爾伯特空間都是巴拿赫空間,但是反之未必。
任何有限維內積空間(如歐幾里德空間及其上的點積)都是希爾伯特空間。但從實際套用角度來看,無窮維的希爾伯特空間更有價值。
內積可以幫助人們從“幾何的”觀點來研究希爾伯特空間,並使用有限維空間中的幾何語言來描述希爾伯特空間。在所有的無窮維拓撲向量空間中,希爾伯特空間性質最好,也最接近有限維空間的情形。
傅立葉分析的一個重要目的是將一個給定的函式表示成一族給定的基函式的和(可能是無窮和)。這個問題可以在希爾伯特空間中更抽象地描述為:任何一個希爾伯特空間都有一族標準正交基,而且每個希爾伯特空間中的元素都可以唯一地表示為這族基中的元素或其倍數的和。
柯西序列
在數學中,一個柯西列是指一個這樣一個序列,它的元素隨著序數的增加而愈發靠近。更確切地說,在去掉有限個元素後,可以使得餘下的元素中任何兩點間的距離的最大值不超過任意給定的正的常數。柯西列是以數學家奧古斯丁·路易·柯西的名字命名的。
定義
設{xn}是距離空間X中的點列,如果對於任意的ε>0,存在自然數N,當m,n>N時,|xn-xm|<ε,稱{xn}是一個Cauchy列。
部分性質
1.對於在某度量空間內的柯西序列,它的極限不一定在相同的度量空間內。如有理柯西序列可導出無理極限。(事實上,一種實數構造就是用這種方法)
2.任何收斂列必然是柯西列,任何柯西列必然是有界序列。
