基函式

介紹

在數學中， 基函式是函式空間中特定基底的元素。函式空間中的每個連續函式可以表示為基函式的線性組合，就像向量空間中的每個向量可以表示為基向量的線性組合一樣。

在數值分析和逼近理論中，基函式也稱為 混合函式，原因是它們用在插值上：把基函式混合起來可作為插值函式（“混合”的方式是根據基函式對數據點的評估）。

例子

多項式基底

多項式基底是將多項式方程式分解為線性函式。

傅立葉基底

正弦和餘弦形成平方可積函式的（正交）Schauder 基。 作為一個特例，該集合為：

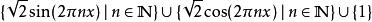基函式

形成一個基底L (0,1).

參見

•線性代數

•線性組合