函式內積

函式的內積用於描述兩個函式之間的關係。它在傅立葉級數中起到了奠基性的作用 ，在其他方面也有用途。

定義

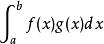函式內積

現規定兩函式f(x)與g(x)與區間[a,b]，且兩函式在該區間上可積且平方可積。則積分 記作函式的內積。函式的內積常記作<f(x),g(x)>。

性質

1、<f,g>=<g,f>

2、<af+bg,h>=a<f,h>+b<g,h>（其中a、b為常數，f、g、h為函式）

3、如果<f,g>在[a,b]上=0，我們就稱f與g在[a,b]上 正交。

對於性質3的證明

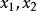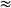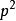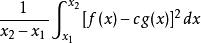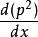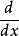函式內積

函式內積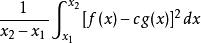

函式內積

函式內積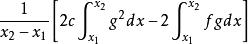

函式內積

函式內積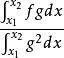

函式內積

函式內積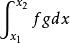

函式內積

函式內積

現有函式f(t)、g(t)，定義在[ ]上，用函式f在g上的分量表示f：f cg，設誤差函式為p=f-cg，用均方誤差法： = ，令 =0，得 { }=0。將積分號中的被積函式展開，並先對其進行求導，整理後得 =0，分離出c，c= 。為使得c=0， 必=0，即<f,g>=0。而c=0也就說明了f在g上的投影為0，而投影為0即為正交。