算法描述
對於 N 位乘數 Y，布斯算法檢查其2的補碼形式的最後一位和一個隱含的低位，命名為 y[i-1] ，初始值為 0 。對於 y[i], i = 0, 1, ..., N - 1，考察 y[i] 和 y[i - 1 ]。當這兩位相同時，存放積的累加器 P 的值保持不變。當 y[i] = 0 且 y[i - 1] = 1 時，被乘數乘以 2^i 加到 P 中。當 y[i]= 1 且 y[i - 1] = 0 時，從 P 中減去被乘數乘以 2^i 的值。算法結束後， P 中的數即為乘法結果。
該算法對被乘數和積這兩個數的表達方式並沒有作規定。一般地，和乘數一樣，可以採用2的補碼方式表達。也可以採用其他計數形式，只要支持加減法就行。這個算法從乘數的最低位執行到最高位，從 i = 0 開始，接下來和 2^i 的乘法被累加器 P 的算術右移所取代。較低位可以被移出，加減法可以只在 P 的前 N 位上進行。
典型實現
布斯算法的實現，可以通過重複地在 P 上加兩個預設值 A 和 S 其中的一個，然後對 P 實施算術右移。設 m 和 r 分別為被乘數和乘數，再令 x 和 y 分別為 m 和 r 中的數字位數。
確定 A 和 S 的值，以及 P 的初始值。這三個數字的總長度應等於( x + y + 1 )：
對於 A ，以 m 的補碼值填充前x位（最靠左的位），用零填滿剩下的( y + 1 )位；
對於 S ，以( - m )的補碼值填充前x位，用零填滿剩下的( y + 1 )位；
對於 P ：用0填滿最左的 x 位，將 r 的值附加在尾部；最右一位用零占位（輔助位，當i=0時i-1=-1,指的就是這個輔助位）；
考察 P 的最右兩位：
如果等於 01，求出 P + A 的值，忽略上溢；
如果等於 10，求出 P + S 的值，忽略上溢；
如果等於 00，不做任何運算，在下一步中直接採用 P 的值；
如果等於 11，不做任何運算，在下一步中直接採用 P 的值。
對第 2 步中得到的值進行算術右移一位，並將結果賦給 P ；
重複第 2 步和第 3 步，一共做 y 次；
舍掉 P 的最右一位，得到的即為 m 和 r 的積。
換另一種說法：把前x位用一個單獨的數R0表示，中間y位用另一個數R1表示，輔助位用Z表示 在這裡，要通過重複的把R0加上m或者減去m來得到結果。具體如下： 初始值R0=0,R1=r.Z=0,此時來考查yi和yi-1這兩位，在這裡就是m的最後一位和Z的值。這裡要說下為什麼每次看的都是這兩位了。 在下邊每次運算後都會把R0,R1,Z中的值右移一次，RO的最後一位移入R1的高位，R1的最後一位移入Z。這裡要注意的是在右移R0時，如果他的最高位是1,則移位後最高位用1填充，如果最高位是0，移位後最高位用0填充。 接下來要按m的最後一位和Z的值來判斷怎么加減了：
如果為01,則R0+m，進位忽略。然後R0,R1,Z右移一位，再下一步判斷，直到把R1的每一位都判斷過後為結束
如果為10,則R0-m，借位忽略（只要x位的R0的值）。然後R0,R1,Z右移一位，再下一步判斷，直到把R1的每一位都判斷過後為結束
如果為00或是11,則R0的值保持不變。然後R0,R1,Z右移一位，再下一步判斷，直到把R1的每一位都判斷過後為結束
最後是結果，結果就是R0並上R1的值。比如R0=3,R1=25,結果就是325.
注意：在實際套用中，“減去m”多用“加上-m”來代替。
算法原理
考慮一個由若干個0包圍著若干個1的正的二進制乘數，比如00111110，積可以表達為：
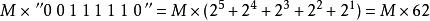布斯乘法算法其中，M代表被乘數。變形為下式可以使運算次數可以減為兩次：
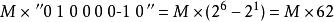布斯乘法算法事實上，任何二進制數中連續的1可以被分解為兩個二進制數之差：
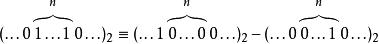布斯乘法算法因此，我們可以用更簡單的運算來替換原數中連續為1的數字的乘法，通過加上乘數，對部分積進行移位運算，最後再將之從乘數中減去。它利用了我們在針對為零的位做乘法時，不需要做其他運算，只需移位這一特點，這很像我們在做和99的乘法時利用99=100−1這一性質。這種模式可以擴展套用於任何一串數字中連續為1的部分（包括只有一個1的情況）。那么，
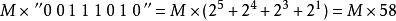布斯乘法算法
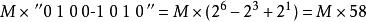布斯乘法算法布斯算法遵從這種模式，它在遇到一串數字中的第一組從0到1的變化時（即遇到01時）執行加法，在遇到這一串連續1的尾部時（即遇到10時）執行減法。這在乘數為負時同樣有效。當乘數中的連續1比較多時（形成比較長的1串時），布斯算法較一般的乘法算法執行的加減法運算少。
