可分

定義

稠密子集

可分

定義1 設（X，ρ）是一個距離空間，集合EX 滿足如下的條件：

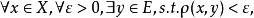可分

就稱E是X 的 稠密子集。

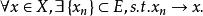可分

可分

註：易見EX 是X的稠密子集的充分必要條件是： 例如根據魏爾斯特拉斯定理，[a，b]上的多項式空間P[a，b]在C[a，b]中稠密。

可分性

定義2 一個距離空間若有可數稠密子集，就稱為是 可分的。

重要結論

定理 完全有界的距離空間是可分的。

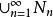可分

證明：取N為有窮的1/n網，則是一個可數稠密子集。

舉例

R 、C[a，b]、L [a，b] (1≤p<∞)均是可分的距離空間，L [a，b]是不可分的距離空間。