多項式乘多項式法則

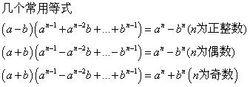多項式乘多項式法則:多項式與多項式相乘，先用一個多項式的每一項與另一個多項式的每一項相乘，再把所得的積相加。

方法

由多項式乘多項式法則可以得到（a+b)(c+d)=a(c+d)+b(c+d)=ac+ad+bc+bd

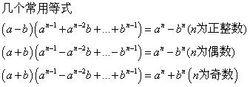多項式乘多項式法則

上面的運算過程，也可以表示為（a+b)(c+d)=ac+ad+bc+bd

多項式乘以多項式就是利用乘法分配律法則得出的。

關於多項式函式的乘積

設P(x)和Q(x)為關於x的多項式函式，其中

P(x) = ∑a_nx^n

Q(x) = ∑b_nx^n

則有

P(x)Q(x) = ∑(a*b)_nx^n

其中 * 表示卷積運算