基本介紹
一階 牛頓-柯特斯閉型積分公式稱為 梯形法則(trapezoidal rule),下面先介紹 牛頓-柯特斯公式。
牛頓-柯特斯公式
牛頓-柯特斯公式(Newton-Cotes formulas)是一種常用的數值積分公式。它的基本策略是用另一個易於積分的近似函式替換被積函式或表格型數據,即
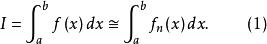 梯形法則
梯形法則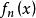 梯形法則
梯形法則其中, 是具有如下形式的多項式
 梯形法則
梯形法則n為多項式的係數。例如,圖1(a)用一次多項式(即直線)作為近似函式;圖1(b)用拋物線作為近似函式。
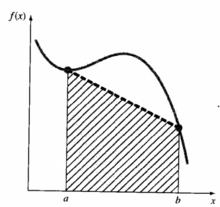 圖1(a)用直線下的面積來逼近積分
圖1(a)用直線下的面積來逼近積分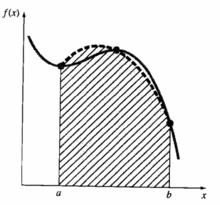 圖1(b)用拋物型下的面積來逼近積分
圖1(b)用拋物型下的面積來逼近積分也可以將整個積分區間分成若干個等距的子區間,每個子區間上使用分段多項式來逼近函式或等距間隔的數據。例如,圖2 使用三個直線段與坐標軸所圍成的面積來逼近積分。還可以使用更高階的多項式去計算積分。
 圖2
圖2牛頓-柯特斯公式分為閉型(closed forms)和開型(open forms)兩類。在積分過程中,如果積分區間兩端的數據點是已知的,則稱為 閉型積分,如圖3(a)所示。反之,若積分區間超出了數據範圍,則稱為 開型積分,如圖3(b)所示。開型公式一般不用於定積分,但可用於計算廣義積分和常微分方程的求解。這裡主要介紹閉型積分公式。
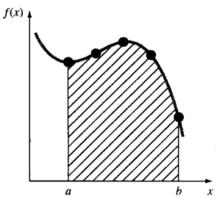 圖3(a)
圖3(a)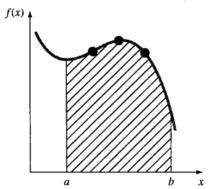 圖3(b)
圖3(b)梯形法則介紹
一階牛頓-柯特斯閉型積分公式稱為 梯形法則(trapezoidal rule),即在式(1)中使用一次多項式
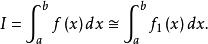 梯形法則
梯形法則我們知道,直線可以表示為
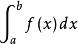 梯形法則
梯形法則用這條直線下的面積作為積分 的一個估計值:
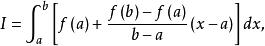 梯形法則
梯形法則積分的結果為
此公式稱為 梯形法則。
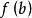 梯形法則
梯形法則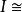 梯形法則
梯形法則 梯形法則
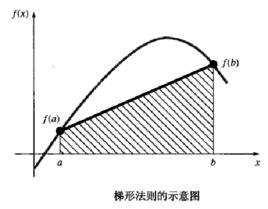
梯形法則如圖4所示,從幾何上看,梯形法則相當於用連線 和 的直線與坐標軸所圍梯形的面積來逼近積分。回顧幾何的知識知,梯形的面積等於高乘以上底和下底的算術平均值(圖5(a))。這個概念在此依然是成立的,只是梯形的方位改變了(圖5(b))。因此,積分公式可近似地表示為: 寬 平均高度,或者 平均高度。
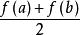 梯形法則
梯形法則其中,對於梯形法則,平均高度等於被積函式在積分區間兩個端點處函式值的算術平均值,即 。
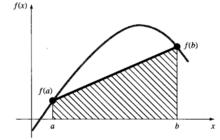 圖4 梯形法則的示意圖
圖4 梯形法則的示意圖所有的牛頓-柯特斯閉型積分公式都可以寫成式( 平均高度)的一般形式。事實上,它們的不同之處僅僅在於對平均高度的計算。
 圖5(a)
圖5(a) 圖5(b)
圖5(b)梯形法則的誤差
很明顯,在使用直線段下的積分逼近曲線積分的過程中,不可避免地會引入誤差(圖6)。對於單套用型梯形法則,對於單套用型梯形法則,近似局部截斷誤差為
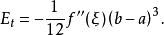 梯形法則
梯形法則 梯形法則
梯形法則其中,介於a,b之間。由上式可以看出,對於所有線性函式,梯形法則精確成立。但對於具有二階或更高階導數(即,有曲率)的函式,誤差總是存在的。
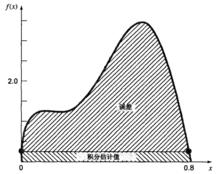 圖6
圖6