方式
常見的函式的圖象變換有四種基本形式：平移變換、對稱變換、伸縮變換和翻折變換。
1 ．平移變換
（ 1 ）橫向平移變換
將函式y=f(x)的圖象沿x軸方向平移 |m|個單位，得到函式y=f(x+m)(m≠0)的圖象， 當m>0時，向左平移；當m<0時，向右平移。
（ 2 ）縱向平移變換
將函式y=f(x)的圖象沿y軸方向平移|n|個單位，得到函式y=f(x)+n(n≠0)的圖象。當n>0時，向上平移；當n<0時，向下平移。
2 ．對稱變換
（1）作函式y=f(x)的圖象關於x軸的對稱圖象，得到函式y=－f(x)的圖象。
（2）作函式y=f(x)的圖象關於y軸的對稱圖象，得到函式y=f(－x)的圖象。
（3）作函式y=f(x)的圖象關於原點的對稱圖象，得到函式y=－f(－x)的圖象。
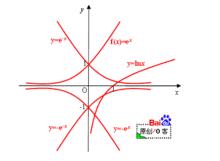圖一.指數函式的圖象變換（4）作函式y=f(x)的圖象關於直線y=x的對稱圖象，得到函式y=f (x)的圖象。
（5）作函式y=f(x)的圖象關於直線x=a的對稱圖象，得到函式y=f (2a－x)的圖象。
如圖一。函式y=e^x的圖象,通過（1）～（4）的變換，分別得到y=－e^x，y=e^（-x），y=－e^(-x)，y=lnx的圖象。
3 ．翻折變換
（1）上下翻折變換
將函式y=f(x)在x軸上方的圖象保留，下方的圖象翻折到上方去，得到函式y=|f(x)|的圖象。
（2）左右翻折變換
將函式y=f(x)在y軸右側的圖象保留，再作其關於y軸的對稱圖象，並去掉y軸左側的原圖象，得到函式y=f(|x|)的圖象。如圖二。函式y=1/e^x的圖象變換得y=1/e^|x|的圖象。
變換
1 ．正弦曲線到正弦型曲線的變換
正弦型函式y=Asin(ωx+φ)，當A≠0, ω≠0, x∈ R時的曲線，可以由正弦曲線y=sinx，通過以下一系列圖象變換而得到：
（1）橫向平移變換
將函式y=sinx的圖象沿x軸向左（當φ≥0時）,向右（當φ<0時）平移|φ|個單位，得到函式y= sin(x+φ)的圖象。
（2）再將函式y= sin(x+φ)的圖象上所有點的橫坐標伸長（當|ω|<1時），縮短（當|ω|>1時）到原來的1/|ω|倍，縱坐標不變，得到函式y=sin(ωx+φ)的圖象。
（3）再將函式y= sin(ωx+φ)的圖象上所有點的縱坐標伸長（當|A|>1時），縮短（當|A|<1時）到原來的|A|倍，橫坐標不變，得到正弦型函式y=Asin(ωx+φ)的圖象。
如圖三。由正弦曲線y=sinx，通過上述變換，得正弦型曲線y=3sin(2x+π/3) 。
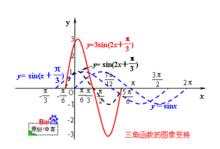圖三.三角函式的圖象變換2 ．簡諧運動的圖象變換
正弦型函式y=Asin(ωx+φ)，當A>0, ω>0,x≥0時，它刻劃的是物理的簡諧運動的位移與時間，交流電的電流與時間的函式關係。
這時，上述變換又可依次稱為（1）相位變換、（2）周期變換、（3）振幅變換。
值得注意的是，若先作周期變換，再作相位變換，則平移量不是|φ|，而是|φ/ω|.
新舊圖象的關係
為簡便起見，我們把變換前的圖象叫舊圖象，變換後的圖象叫新圖象。
1 ．對應觀點
上述變換，除翻折變換的第（2）項左右翻折變換外，其他的變換，新圖象和舊圖象上的點存在一一對應關係。這是我們解決新舊圖象關係的最基本最關鍵的出發點。也是解決其對應的新舊解析式的最基本最關鍵的出發點。
2 ．數形結合觀點
函式的圖象變換，是從“形”的角度使函式發生變化。新舊圖象表示兩個函式。與之對應的兩個函式的解析式也從“式”的角度發生了變化。
3 ．保距性
在上述圖象變換中，平移變換和對稱變換能保持圖形上任何兩點之間的距離不變。可以看成“保距”變換。
但是，翻折變換和伸縮變換不具有這一性質 。
4 ．可逆性
每種形式的函式的圖象變換都有它自己的變換意義，按照它的變換意義將一個函式y=f(x)的圖象以變成另一個函式y=h(x)的圖象，這是它的正向意義。而根據“相反意義”實施逆變換，將函式y=h(x)的圖象變成函式y=f(x)的圖象，這是它的逆向意義。函式的圖象變換具有雙向意義 。
幾點說明
1 ．圖象變換的本質
函式圖象變換的本質，是用圖象的形式表示的函式，由一個函式變化到另一個函式。即新舊圖象是兩個函式。
2． 圖象變換體現的數學思想
函式圖象變換的過程體現了由簡單到複雜，特殊到一般的化歸思想。
3． 圖象變換的基本元素
函式圖象變換的基本元素是自變數“x”。解答有關圖象變換的問題時，“確保x的係數是1”是避免出現錯誤的重要策略 。
4.參考資料
[1]中學數學教師手冊
[2]高中課程標準實驗教科書數學
[3]高中數學教師教學用書
[4]高中數學函式
[5]高等數學手冊
