固體狀態方程
正文
描述固體壓力p、體積V、溫度T之間關係的函式。狀態方程的物理基礎是熱力學第一定律和第二定律。當外界對固體作功dW,以及固體從外界吸收熱量TdS後，其內能U發生dU的變化,自由能F=U+TS,則有dF的變化：
。
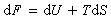等溫狀態方程 根據兩種情況，分別考慮。
① 有限應變理論。這是一種不考慮固體結構特點、把固體當成連續彈性體，並從默納漢有限應變理論出發，導出狀態方程的方法。常見的這類方程有：
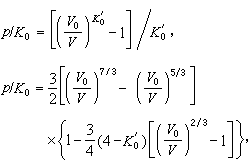
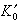各為壓力為零時的體彈性模量和該模量對壓力的導數。 還有布里奇曼狀態方程其形式為：
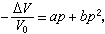
② 從固體結構特點導出的等溫狀態方程。這種方法是基礎是從詳細的固體原子和電子結構知識出發，計算自由能，然後利用該自由能計算狀態方程。在不考慮溫度效應時，該能量主要成分是點陣能和零點能。一般固體的零點能比點陣能小很多，只在鍵比較弱的稀有氣體的凝聚態中才例外。離子晶體的點陣能主要由離子間的庫侖作用決定。分子晶體則主要由原子或分子的范德瓦耳斯力決定。平衡這些相互作用的排斥勢由實驗確定。金屬的點陣能由自由電子的動能和交換能、電子和離子之間的庫侖能，以及離子間的排斥能之和構成。
高溫狀態方程 以上的處理都沒有考慮溫度這一因素，當考慮溫度效應時，則必須計入激發態對自由能的貢獻。這些激發包括原子熱振動、電子和自鏇的熱激發，以及分子轉動等等。由於它們產生了熱壓力，引出了熱狀態方程。
① 原子熱振動。E.格臨愛森在處理原子熱振動對自由能貢獻時，把整個固體原子的熱振動處理成簡諧振動的疊加，這時固體的自由能為：
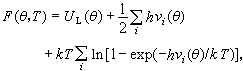
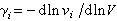相等都是γ，於是可以得到米－格臨愛森熱狀態方程：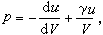 
從德拜理論出發，也能導出類似的熱狀態方程。但這時
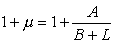其中嘷為德拜溫度，vm為德拜極限頻率。 ② 電子熱激發。金屬自由電子的熱激發也會對自由能有貢獻。按金屬自由電子模型把傳導電子看作理想氣體粒子，並遵從費密-狄喇克統計,最後可以得到金屬中熱激發傳導電子產生的熱壓力為：
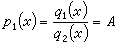
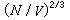，所以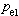
隨密度的三分之一次方改變。 超高壓狀態方程──統計方法 以上的固體狀態方程都是以可以找到描述點陣能模型為前提的。這種模型對於不同固體是不同的。但是當壓力不斷增加，原子間相互作用力的細節變得不那么重要時，可以採用托馬斯-費密－狄喇克(TFD)統計模型描述狀態方程。這種方法適用於原子序數大，壓力非常高的情況。
① 絕對零度時的TF模型。這是以簡併電子氣方式描述原子中的電子的統計方法。它假設:(1)電子首先是受原子核中心勢場V(r)的作用。當原子中有多個電子共存時,V(r)略作改變；（2）電子服從費密-狄喇克統計；(3)電子電荷密度連續分布,核周圍連續分布的電子云勢函式滿足泊松方程。根據自由電子氣動力學理論，壓力
，
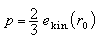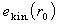為原子半徑ro 處的動能密度。最後得到TF狀態方程為： 
。
，
，
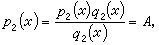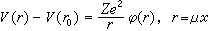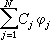② TF模型的溫度微擾。溫度的效應是改變原子內部的電子分布。通過費密-狄喇克統計計算,最後得到一級溫度微擾下的TF狀態方程為：
,
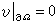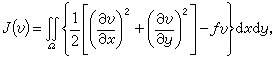嗞o為溫度為零時TF函式在邊界上的值。 ③ TFD模型。上述TF模型假定核周圍是簡併電子氣，除靜電禁止作用外，沒有考慮電子間的其他相互作用。當計入電子自鏇之間的交換作用得到托馬斯-費密-狄喇克(TFD)狀態方程為
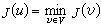
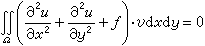，ψ(xo)是ψ在原子表面處的邊界值。 在非常高密度情況下，電子動能超過勢能，變為主要貢獻。在溫度不太高時,則壓力
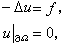N是物體中總電子數,UF為費密能量（見費密面）。在更高壓力下，則必須考慮原子核捕獲電子而引起相對論性效應和核反應。 參考書目
L. Knopoff, Equation of State of Solids at Moderately High Pressure, R.S. Bradley, ed., High Pressure Physics and Chemistry, Vol.1, pp.227～244, Academic Press, London and New York, 1963.
L. Knopoff, Equation of State of Solids at Ultra-High pressures. R. S. Bradley, ed., High Pressure and Chemistry, Vol. 1, pp. 247～262. Academic Press, London and New York, 1963.
L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press, Oxford, 1958.
