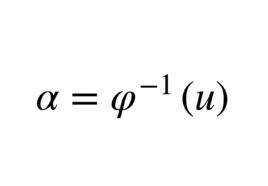定義介紹
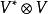 單位張量
單位張量 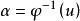 單位張量
單位張量 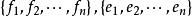 單位張量
單位張量 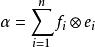 單位張量
單位張量 單位張量是合成代數的單位元。設V*,V是域K上的對偶空間,是V*與V的合成代數。對任意的 a*∈V*, b∈V,定義φ:V*⊗V→(V,V), a*⊗ b⟼φ( a*⊗ b),其中φ( a*⊗ b)( x)=⟨ a*, x⟩⊗ b是個線性映射,這樣φ是個代數同態,且是單射。若dim V=n,則φ是線性同構。若u是V上的單位映射,則是合成代數V*⊗V的單位元,稱為V的單位張量,如果是V*與V的一對對偶基,那么,且與對偶基的選取無關。
合成代數
[composition algebra]
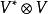 單位張量
單位張量 一類由對偶空間的張量積所構成的代數。設V*,V是域K上的對偶空間,對任意的x,y∈V,x*,y*∈V*,定義上的乘法
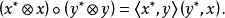 單位張量
單位張量 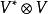 單位張量
單位張量 該運算使得成為一個非交換的結合代數,稱為V*與V的合成代數。
張量
張量理論是數學的一個分支學科,在力學中有重要套用。張量這一術語起源於力學,它最初是用來表示彈性介質中各點應力狀態的,後來張量理論發展稱為物理學的一個有利的數學工具。
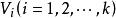 單位張量
單位張量 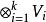 單位張量
單位張量 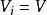 單位張量
單位張量 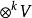 單位張量
單位張量 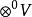 單位張量
單位張量 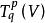 單位張量
單位張量 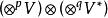 單位張量
單位張量 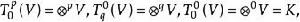 單位張量
單位張量 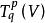 單位張量
單位張量 設是域K上的向量空間,則稱(特別地,當所有時,記作)中的元素為張量。為了符號的方便,我們用表示K。令V*為V的對偶空間,用記,並設稱中的元素為V上的p次反變q次共變張量或(p,q)型張量。
張量的內積
張量的內積指由兩個張量中其一張量的反變指標與另一張量的共變指標的乘積所得的收縮張量。