公式表達
 並矢張量
並矢張量 並矢張量
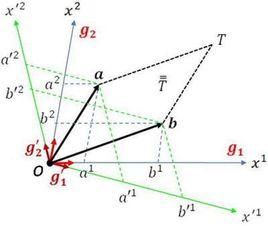
並矢張量例如,設定兩個三維向量和,
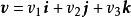 並矢張量
並矢張量,
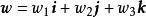 並矢張量
並矢張量;
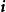 並矢張量
並矢張量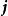 並矢張量
並矢張量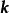 並矢張量
並矢張量其中,、、,形成了一個三維空間裡的標準正交基的單位基底向量。
 並矢張量
並矢張量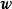 並矢張量
並矢張量那么,與並置成為
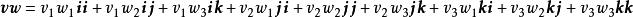 並矢張量
並矢張量;
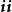 並矢張量
並矢張量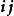 並矢張量
並矢張量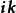 並矢張量
並矢張量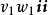 並矢張量
並矢張量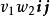 並矢張量
並矢張量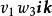 並矢張量
並矢張量其中,、、等等,都是單位並矢,、、 等等,都是並矢。
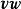 並矢張量
並矢張量並矢張量也可以表達為
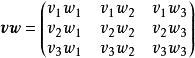 並矢張量
並矢張量。
定義
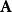 並矢張量
並矢張量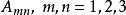 並矢張量
並矢張量根據Morse與feshbach所著作的教科書,在三維空間裡,並矢張量是一個3×3陣列,其分量,當從一個坐標系變換到另外一個坐標系時,遵守協變變換(covariant transformation)的定律。
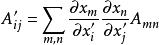 並矢張量
並矢張量;
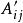 並矢張量
並矢張量其中,是變換後的分量。
所以,並矢張量是一個二階協變張量。反過來說,按照這定義推廣,任意二階協變張量都是並矢張量:
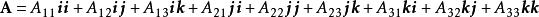 並矢張量
並矢張量。
並矢張量運算
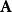 並矢張量
並矢張量 並矢張量
並矢張量套用點積,並矢張量可以與向量綜合在一起:
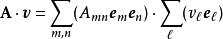 並矢張量
並矢張量;
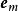 並矢張量
並矢張量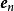 並矢張量
並矢張量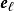 並矢張量
並矢張量其中,、、,都是標準正交基的基底向量。
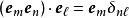 並矢張量
並矢張量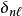 並矢張量
並矢張量注意到;其中,是克羅內克函式。所以,
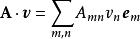 並矢張量
並矢張量;
這點積運算得到的結果是一個協變向量。
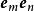 並矢張量
並矢張量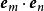 並矢張量
並矢張量並矢張量的縮並(tensor contraction)運算,將每一個並置,替換為兩個單位基底向量的點積,以方程式表達為
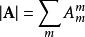 並矢張量
並矢張量。
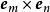 並矢張量
並矢張量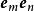 並矢張量
並矢張量只成立於三維空間,並矢張量的 旋轉因子運算,將每一個並置,替換為兩個單位基底向量的叉積,以方程式表達為
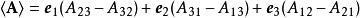 並矢張量
並矢張量。
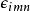 並矢張量
並矢張量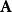 並矢張量
並矢張量這也可以表達為與列維-奇維塔符號的完全縮並:
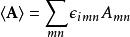 並矢張量
並矢張量。
進階理論
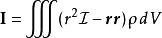 並矢張量
並矢張量 並矢張量
並矢張量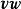 並矢張量
並矢張量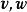 並矢張量
並矢張量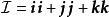 並矢張量
並矢張量兩個向量的 並矢積其實就是張量積。 兩個並矢積作形式上的相加就是 並矢張量,從而並矢張量和二階張量(嚴格地說,是二階的反變張量)是同義詞。力學、電動力學中常見的例子就是單位並矢張量、轉動慣量以及馬克士威應力張量等;量子力學中的角動量耦合(angular momentum coupling)理論也要用到並矢張量。
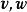 並矢張量
並矢張量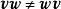 並矢張量
並矢張量需要注意:並矢積是不可交換的,也就是說,除非兩個矢量線性相關,否則一定有。
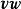 並矢張量
並矢張量 並矢張量
並矢張量在物理學中,並矢張量最重要的套用之一就是它和向量的縮並。對於並矢積和向量的縮並,規定
 並矢張量
並矢張量。
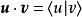 並矢張量
並矢張量如果要求這種規定也適用於量子力學中的態矢量,在這種情況下就要特別注意每個式子右端各個向量的先後順序:用狄拉克符號來寫,則。
範例
旋轉
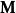 並矢張量
並矢張量設定為一個並矢張量:
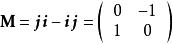 並矢張量
並矢張量。
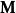 並矢張量
並矢張量是一個二維空間的 90°旋轉運算元(rotation operator) 。它可以從左邊點積一個向量來產生一個旋轉:
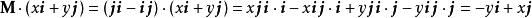 並矢張量
並矢張量;
或以矩陣表達,
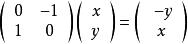 並矢張量
並矢張量。
 並矢張量
並矢張量一個一般的二維旋轉並矢張量,會產生角度反時針方向的旋轉,表達為
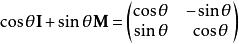 並矢張量
並矢張量;
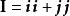 並矢張量
並矢張量其中,是二維的 單位並矢張量。
量子力學
 並矢張量
並矢張量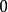 並矢張量
並矢張量 並矢張量
並矢張量 並矢張量
並矢張量 並矢張量
並矢張量 並矢張量
並矢張量 並矢張量
並矢張量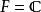 並矢張量
並矢張量 並矢張量
並矢張量 並矢張量
並矢張量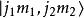 並矢張量
並矢張量設是量子力學中所有的角動量本徵態所張成的希爾伯特空間(囊括了所有可能的總角動量量子數,,,,),則。當我們要考慮角動量耦合的時候,就會遇到態矢量的並矢張量,而且時常把它記作或等等。任取一些複數(但是其中只能有有限個非零),則
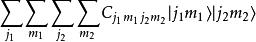 並矢張量
並矢張量 並矢張量
並矢張量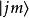 並矢張量
並矢張量就是一個並矢張量。不妨把這個並矢張量記作,則它和的縮並就是
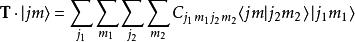 並矢張量
並矢張量,
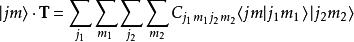 並矢張量
並矢張量。
 並矢張量
並矢張量 並矢張量
並矢張量在這其中,量子力學中最廣為人知的就是通過CG矢量耦合系 數(Clebsch-Gordan coefficients) 所組合出來的張量。當然,在角動量耦合理論中,這樣的張量被等同為某些角動量本徵態,除了物理上的考慮之外,這更主要地還是有關李群及其李代數的表示的另外一個話題,請參看李群的表示(Lie group representation) 及李代數的表示(Lie algebra representation) ,在這裡就不再深入探討了。
實際上可以這樣說,在量子力學中,只要物理問題涉及了系統的耦合,數學上就會導致態矢量的並矢。在這方面,還可以舉一個常見的例子:由一維諧振子的態矢量所構成的並矢張量可以用來描述二維諧振子系統。
經典力學
三維歐幾里得空間上的並矢張量的例子非常多,例如轉動慣量、應力張量、應變等等。這些例子實際上就是並矢張量這個概念的最初原型。