(協變)張量的定義
坐標系的變換關係
僅討論笛卡兒右手直角坐標系。
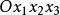 協變張量
協變張量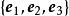 協變張量
協變張量舊坐標系: 單位基矢量: ;
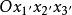 協變張量
協變張量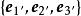 協變張量
協變張量新坐標系: 單位基矢量: ,如圖1所示 。
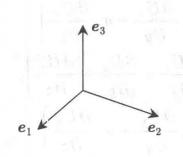 圖1(a)標架變換
圖1(a)標架變換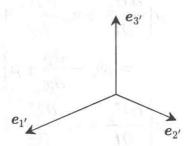 圖1(b)標架變換
圖1(b)標架變換新舊基矢量夾角的方向餘弦:
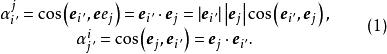 協變張量
協變張量坐標系的(標架)變換關係(舊錶新):
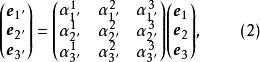 協變張量
協變張量其中
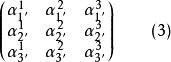 協變張量
協變張量為變換係數矩陣,(2)也可表示為
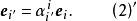 協變張量
協變張量坐標系的(標架)變換關係(新表舊):
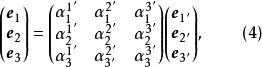 協變張量
協變張量其中
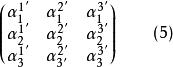 協變張量
協變張量為矩陣(3)的逆,(4)也可表示為
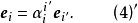 協變張量
協變張量標量(純量Scalar)
標量在坐標變換時其值保持不變,即滿足
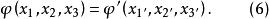 協變張量
協變張量如數學中的純數,物理中的質量、密度、溫度等。
問題:時間是否標量?(答案:是標量,可以用一個數字表示。)
注 標量是0階張量。
協變矢量
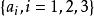 協變張量
協變張量矢量在坐標變換時一般要改變,滿足以下變換關係的三個量 定義一個矢量:
 協變張量
協變張量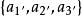 協變張量
協變張量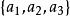 協變張量
協變張量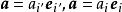 協變張量
協變張量設為任意矢量,其在新、舊坐標系下的(協變)分量分別為 和 ,即 ,所以
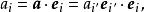 協變張量
協變張量得
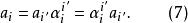 協變張量
協變張量而
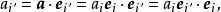 協變張量
協變張量得
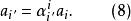 協變張量
協變張量可見矢量的變化規律與坐標架變換(2)一致,故為 協變。代人上式(換啞指標),
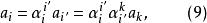 協變張量
協變張量得
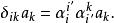 協變張量
協變張量比較上式兩邊,得
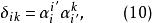 協變張量
協變張量即該變換是正交的。
推廣到協變張量
將矢量定義加以推廣:(增加指標和相應的變換係數)
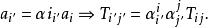 協變張量
協變張量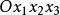 協變張量
協變張量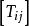 協變張量
協變張量對於直角坐標系 ,有9個量 按照(協變)關係
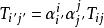 協變張量
協變張量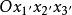 協變張量
協變張量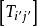 協變張量
協變張量變換成 ,中的9個量 ,則此9個量定義一個二階(協變)張量。
各階(協變)張量小結:
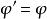 協變張量
協變張量——零階張量(標量)
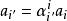 協變張量
協變張量——一階張量(向量)
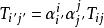 協變張量
協變張量——二階張量
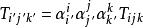 協變張量
協變張量——三階張量
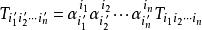 協變張量
協變張量——n階張量
二階張量的另一種定義:
 協變張量
協變張量二階張量T是把任意一個矢量 變換成另一個矢量 b的線性變換,表達式為
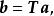 協變張量
協變張量而且具有下列線性性質:
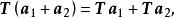 協變張量
協變張量加法:
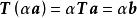 協變張量
協變張量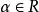 協變張量
協變張量標乘: (其中 ) 。
向量空間的張量代數
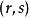 協變張量
協變張量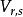 協變張量
協變張量向量空間的張量代數(tensor algebra of vector space)是由向量空間與其對偶空間的張量積直和所構成的代數。向量空間V的 型張量空間 定義為
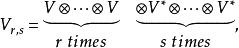 協變張量
協變張量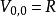 協變張量
協變張量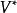 協變張量
協變張量其中 , 是V的對偶空間,對於這樣一些向量空間取直和
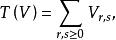 協變張量
協變張量則在張量積的運算之下,T(V)成為一個代數,稱為向量空間V的 張量代數 。
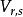 協變張量
協變張量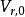 協變張量
協變張量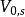 協變張量
協變張量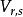 協變張量
協變張量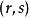 協變張量
協變張量T(V)中的元素稱為 張量,它是各個 中的元素關於R的有限線性組合, 中的元素稱為 r階反變張量, 中的元素稱為 s階協變張量, 中的元素稱為 階 齊次張量。
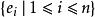 協變張量
協變張量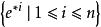 協變張量
協變張量設 與 分別是V和V*彼此對偶的基底,則
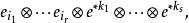 協變張量
協變張量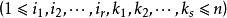 協變張量
協變張量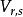 協變張量
協變張量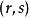 協變張量
協變張量是 的基底。因此, 型張量x可以惟一地表成
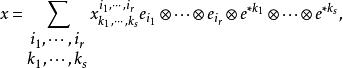 協變張量
協變張量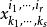 協變張量
協變張量其中 稱為張量x在上述基底下的分量。
處理張量時,通常採用愛因斯坦的和式約定:在一個單項表達式中出現重複的上、下指標,表示該式關於這個指標在它的取值範圍內求和,而略去和號不寫,採用這個約定,上述張量x可寫成
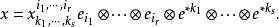 協變張量
協變張量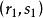 協變張量
協變張量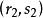 協變張量
協變張量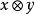 協變張量
協變張量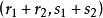 協變張量
協變張量設x是 型張量,y是 型張量,則它們的積 是 型張量 。

