麥克斯韋脅強張量

麥克斯韋脅強張量 J.C.麥克斯韋用以說明電磁場彈性力學性質的張量。在19世紀關於電荷之間相互作用力的問題上，曾有“超距作用”及“近距作用”兩種論點。前者認為相互作用無需經過媒質；後者認為必需藉助於媒質。但真空中沒有通常的媒質，於是提出以太論。

麥克斯韋脅強張量

正文

J.C.麥克斯韋用以說明電磁場彈性力學性質的張量。在19世紀關於電荷之間相互作用力的問題上，曾有“超距作用”及“近距作用”兩種論點。前者認為相互作用無需經過媒質；後者認為必需藉助於媒質。但真空中沒有通常的媒質，於是提出以太論。假定空間充滿了無質量但有彈性的“以太”，靠它傳遞作用力和傳播波動。為了描述電荷之間作用力,M.法拉第提出力線管概念:每個力線管包含大量的力線，用單位橫截面內力線的數目來標誌電場強度，並認為這些力線管縱向有張力，橫向有壓力。力線起始於正電荷而終止於負電荷，異號電荷間的吸力和同號電荷間的斥力即通過力線管的縱向張力和橫向壓力進行傳遞。磁場的情形也類似，沿磁力管方向存在張力，垂直於磁力管方向存在壓力。麥克斯韋用數學方法證明了法拉第觀點，得出了一個類似於彈性力學的方程。其中與脅強相當的張量，稱為麥克斯韋脅強張量。它可以用電場E和磁場H表示出來,並分為電和磁兩部分，分別以分量來表示,忽略介質的電致伸縮和磁致伸縮，並用高斯單位制

ε為介電常數（或電容率），μ 為磁導率，δik為克羅內克符號，
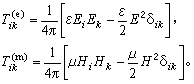
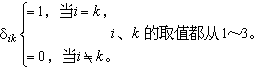
在彈性體內，徹體力密度F) 與脅強張量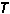的關係為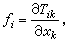 對一封閉曲面S內的體積V求積分得到給定體積里所受的總力等於S面上脅強的面積分，即

從近代場論的觀點看，雖然以太並不存在，但電磁場具有物質性並具有能量和動量，電荷之間的作用是通過電磁場傳遞的。法拉第和麥克斯韋所構想的脅強相當於電磁場的動量流。因此麥克斯韋脅強張量在近代電磁場理論或電動力學書中又稱為電磁場動量流張量，只是增加了一個負號（這是由於定義上的差別）。

配圖

相關連線