定義
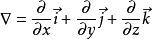哈密頓運算元哈密頓（W.R.Hamiltonian）引進了一個矢性微分運算元： ，稱之為哈密頓運算元或者▽ 運算元。
記號▽ 讀作“那勃樂（Nzbla）”，在運算中既有微分又有矢量的雙重運算性質，其優點在於可以把對矢量函式的微分運算轉變為矢量代數的運算，從而可以簡化運算過程，並且推導簡明扼要，易於掌握。
▽ 本身並無意義，就是一個運算元，同時又被看作是一個矢量，在運算時，具有矢量和微分的雙重身份。
運算規則
3個等式
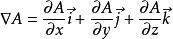哈密頓運算元（1） ，這樣標量場A通過▽的這個運算就形成了一個矢量場，該矢量場反應了標量場A的分布。
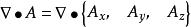哈密頓運算元（2）
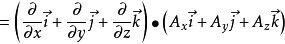哈密頓運算元
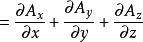哈密頓運算元；
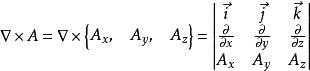哈密頓運算元（3）
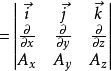哈密頓運算元
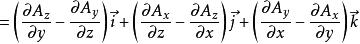哈密頓運算元。
與梯度、散度、旋度的關係
數量（標量）場的梯度與矢量場的散度和旋度可表示為：
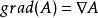哈密頓運算元（1） ；
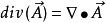哈密頓運算元（2） ；
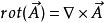哈密頓運算元（3） 。
與拉普拉斯運算元的關係
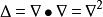哈密頓運算元常用公式
準備工作
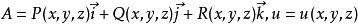哈密頓運算元設，首先引入新的矢性微分運算元，如下所示：
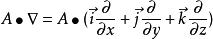哈密頓運算元
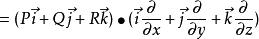哈密頓運算元
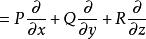哈密頓運算元它既可以作用在數性函式 u=u(M) 上，又可以作用在矢性函式 B(M) 上。
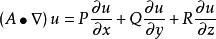哈密頓運算元（1）；
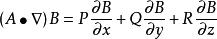哈密頓運算元（2）。
需要注意的是：
哈密頓運算元
哈密頓運算元（1）與 是完全不同的；
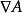哈密頓運算元
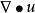哈密頓運算元（2）與是無意義的。
公式匯總
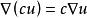哈密頓運算元（1）；
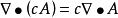哈密頓運算元（2）；
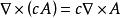哈密頓運算元（3）；
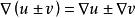哈密頓運算元（4）；
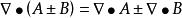哈密頓運算元（5）；
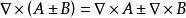哈密頓運算元（6）；
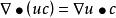哈密頓運算元（7）；
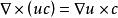哈密頓運算元（8）；
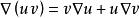哈密頓運算元（9）；
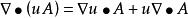哈密頓運算元（10）；
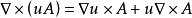哈密頓運算元（11）；
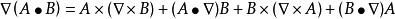哈密頓運算元（12）；
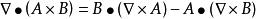哈密頓運算元（13）；
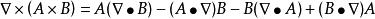哈密頓運算元（14）；
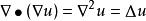哈密頓運算元（15）；
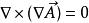哈密頓運算元（16）；
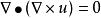哈密頓運算元（17）；
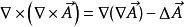哈密頓運算元
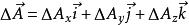哈密頓運算元（18），其中。
