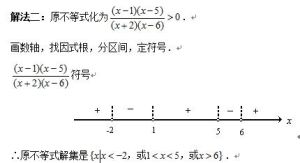
同解不等式

如果兩個不等式的解集相同，那么這兩個不等式叫做同解不等式。不等式的基本性質是所有不等式都具有的，而同解不等式的同解原理是條件不等式中所特有．因為只有條件不等式才有不等式的解集。

同解不等式

同解不等式

如果兩個不等式的解集相同，那么這兩個不等式叫做同解不等式．

同解不等式的基本性質

①不等式F（x）＜ G（x）與不等式 G（x）＞F（x）同解。

②如果不等式F（x）＜ G（x）的定義域被解析式H（ x ）的定義域所包含，那么不等式 F（x）＜G（x）與不等式F（x）＋H（x）＜G（x）＋H（x）同解。

③如果不等式F（x）＜G（x）的定義域被解析式H（x）的定義域所包含，並且H（x）＞0，那么不等式F(x)＜G（x）與不等式H（x）F（x）＜H（ x ）G（x）同解；如果H（x）＜0，那么不等式F（x）＜G（x）與不等式H (x)F（x）＞H（x）G（x）同解。

（1）不等式的基本性質是所有不等式都具有的，而同解不等式的同解原理是條件不等式中所特有．因為只有條件不等式才有不等式的解集．(2)把不等式中的任何一項改變其符號後，從不等號的一邊移到另一邊，所得的不等式與原不等式是同解不等式．解不等式。