定義
經過合併同類項後,未知數的最高次數是1的整式所組成的不等式就是一次不等式,又叫 線性不等式。一次不等式中若含有n個未知數,則稱為n元一次不等式。n元一次不等式的標準形式為
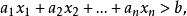 一次不等式
一次不等式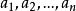 一次不等式
一次不等式其中 不全為零。常見的問題是解一元一次不等式、二元一次不等式組等 。
一元一次不等式
概念
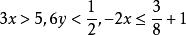 一次不等式
一次不等式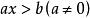 一次不等式
一次不等式只含有一個未知數,並且未知數的次數是1、係數不等於0的整式不等式,叫作 一元一次不等式,如等。一元一次不等式的解集為:
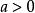 一次不等式
一次不等式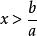 一次不等式
一次不等式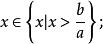 一次不等式
一次不等式(1)當時,解為,則
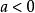 一次不等式
一次不等式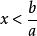 一次不等式
一次不等式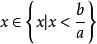 一次不等式
一次不等式(2)當時,解為,則。
註:以上“>”可換成“≥”,同樣,“<”可換成“≤”。
解題步驟
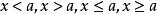 一次不等式
一次不等式解一元一次不等式,要根據不等式的基本性質,將不等式逐步化為 的形式,一般步驟為 :
(1)去分母;(2)去括弧;(3)移項;(4)合併同類項;(5)係數化為1。
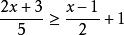 一次不等式
一次不等式例1 解不等式: 。
解:原不等式 去分母,得
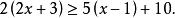 一次不等式
一次不等式去括弧,得
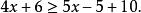 一次不等式
一次不等式移項,得
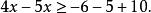 一次不等式
一次不等式合併同類項,得
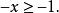 一次不等式
一次不等式係數化為1,兩邊同除以一1,得
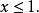 一次不等式
一次不等式所以原不等式的解集為
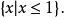 一次不等式
一次不等式二元一次不等式(組)
二元一次不等式
 一次不等式
一次不等式含有兩個未知數,並且未知數的最高次數是1的不等式稱為 二元一次不等式。例如等。
二元一次不等式組
由幾個二元一次不等式組成的不等式組稱為二元一次不等式組。
二元一次不等式(組)的解集
 一次不等式
一次不等式 一次不等式
一次不等式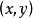 一次不等式
一次不等式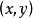 一次不等式
一次不等式滿足二元一次不等式(組)的 和 的取值構成有序數對 ,所有這樣的有序數對 構成的集合稱為 二元一次不等式 (組)的解集。
二元一次不等式(組)的幾何意義
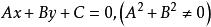 一次不等式
一次不等式在平面直角坐標系中,平面內的所有點都被直線分成三類。
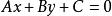 一次不等式
一次不等式第一類:在直線上的點;
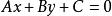 一次不等式
一次不等式第二類:在直線上方區域內的點;
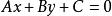 一次不等式
一次不等式第三類:在直線下方區域內的點。
簡單線性規劃
 一次不等式
一次不等式約束條件:由的不等式(或方程)組成的不等式組。
 一次不等式
一次不等式線性約束條件:由的一次不等式(或方程)組成的不等式組。
 一次不等式
一次不等式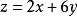 一次不等式
一次不等式目標函式:關於的函式的解析式,如等。
 一次不等式
一次不等式線性目標函式:關於的一次解析式。
 一次不等式
一次不等式可行解:滿足線性約束條件的解。
可行域:所有可行解組成的集合。
最優解:使目標函式取得最大值或最小值的可行解。
線性規劃 問題:求線性目標函式線上性約束條件下的最大值或最小值問題 。

