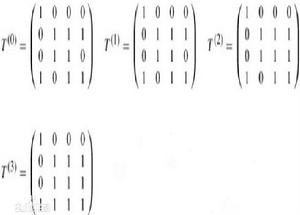可達矩陣

可達矩陣，指的是用矩陣形式來描述有向連線圖各節點之間經過一定長度的通路後可達到的程度。可達矩陣的計算方法是利用布爾矩陣的運算性質。 可達矩陣對應的是拓撲幾何，而不是通常講的幾何。它描述的是要素之間的相對位置的關係。跟具體的幾何坐標無關。 裡面的布爾矩陣，指的是方陣，矩陣中的第i行與第i列對應同一個要素。

基本信息

• 中文名：可達矩陣
• 其他外文名：無
• 類型：數學問題
• 計算公式：利用布爾矩陣的運算性質

可達矩陣

是用矩陣形式來描述有向連線圖各節點之間經過一定長度的通路後可達到的程度。

在實際系統建模工程中，有向圖D={S,R}中，對於Si,Sj 屬於S，如果從Si到Sj有任何一條通路存在，則可稱Si可達Sj。

利用布爾矩陣的運算性質給出了計算有向圖可達矩陣的方法,該方法計算簡便.

對於可達矩陣求解方法有如下幾種方式：

1、連乘法：

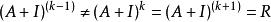可達矩陣

其中A為原始鄰接布爾矩陣，I為單位矩陣，R為可達矩陣

2、冪乘法：

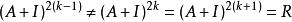可達矩陣

3、warshall算法：

通過轉移矩陣的方式計算出可達矩陣

4、疊代warshall算法

對每個要素進行warshall操作後，記錄其狀態，下個要素疊代時候是以當前狀態為基礎進行疊代

5、tarjan算法 求出所有強連通分量後一次性疊代warshall算法即可

上述五種方法中，最後一種方法比前面四種方法運算速度上有數量級的提高。對於普通的100*100的鄰接矩陣，其速度大致提高100倍左右。