基本介紹
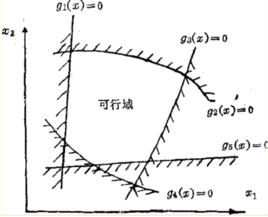
所謂 約束集合,就是指所有不等式約束和等式約束的交集。在此集合內所有設計點x都滿足全部的約束條件,故又稱它為 設計可行域,表示為:
 可行域
可行域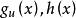 可行域
可行域其中假設函式 和h(x)都是連續的。這樣,對於一個約束的最佳化設計問題,由於約束面的存在而把設計空間劃分為兩個區域: 設計可行域D和 非可行域。因而,最優解或可接受設計解只能從可行域內的各點中產生。
顯然,若在可行域內不存在設計點,則認為此可行集合是個 空集,此時也就得不到一個設計解,問題就可能出於所建立的約束條件與設計要求是相矛盾的。
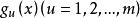 可行域
可行域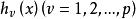 可行域
可行域關於約束可行域D是否為一個凸集,在凸規劃理論中證明了:若各個不等約束函式 是凸函式和等式約束 是線性函式,則D是凸集。但是只要等式約束是非線性的,那么集合D一定是個非凸集。
可行域的其他性質
【例1】對於一個二維問題,當其約束條件為:
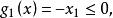 可行域
可行域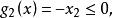 可行域
可行域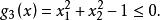 可行域
可行域由圖1 (a)可見,它是一個在第一象限內的凸集;當約束條件改為:
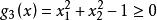 可行域
可行域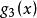 可行域
可行域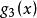 可行域
可行域時,由圖1 (b)可見,是一個在第一象限內的非凸集D,因為函式是一凹函式;當約束條件取為等式約束
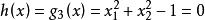 可行域
可行域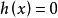 可行域
可行域時,由圖1 (c)可見,也是一個非凸集,此時這個集合是在x≥0和x≥0(第一象限內)上的一段曲線。
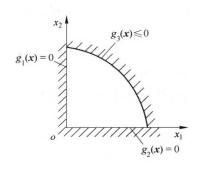 圖1(a)凸集
圖1(a)凸集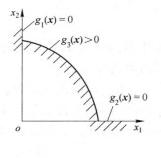 圖1 (b)非凸集
圖1 (b)非凸集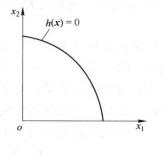 圖1(c)非凸集
圖1(c)非凸集值得注意的是,一個約束函式經過變換,雖然表示形式不同但未改變其約束條件的性質,但有時卻會影響約束函式的凸性,例如,對於x>0和x>0,且a和b為正常數,其原約束條件形式為:
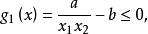 可行域
可行域可以等價地變換為下面形式(由於x和x均取正值,故不等式的意義沒有改變):
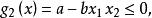 可行域
可行域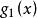 可行域
可行域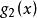 可行域
可行域結果是是凸函式,變換為則是非凸函式,因為它們的Hessian矩陣分別為:
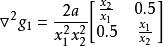 可行域
可行域和
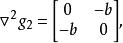 可行域
可行域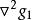 可行域
可行域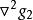 可行域
可行域式中,為正定矩陣;為不定矩陣。
由此,約束函式通過形式上的變換,結果可能丟失了函式的凸性(或者相反),這也就影響可行域的約束集合的凸性條件。
根據上述可以推知,在n維歐氏空間R 中,由一組不等式約束函式可以組成一個或幾個可行域D。對於僅由一組等式約束所組成的可行域D,如果這組方程的函式是連續且彼此獨立的,那么這個可行域D就是一個n-p維的子集。
對於由一組非線性約束函式所定義的可行域,確定它是凸集還是非凸集,一般說來是比較困難的,而且對於一個非凸的集合,往往是造成一個最佳化設計問題有多個約束極值的重要原因。