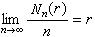正文
研究實數的分數部分在區間
=【0,1)中的分布問題。一致分布理論的發展則開始於H.外爾1916年關於一致分布理論的著名研究。一致分布除自身的發展外,在解析數論、機率論和近似分析中都有重要的套用。例如,關於外爾和估計的研究是解析數論與堆壘數論中的核心。
命
(
=1,2,…)為
中的一個點集。對於任意正整數
及任意實數
∈
,命
(
)表示
個點
(1≤
≤
)落入區間【0,
)的點的個數。如果
,
則稱點集
(
=1,2,…)在
中一致分布。
外爾給出了判斷一致分布的重要法則,即所謂外爾判別法:點集
(
=1,2,…)在
中一致分布的充分必要條件為,對於任一
中的黎曼可積函式
(
),皆有
。
套用這一法則十分困難,因為需對所有黎曼可積函式進行研究才能證明點集的一致分布性,於是導致外爾在黎曼可積函式的集合中,選出一個特殊的序列
,
其線性包給出每一黎曼可積函式。從而他證明了下面更精密的判別法:數列
(
=1,2,…)在
中一致分布的充分必要條件為,對於任意整數
≠0,常有
。
例如,對於任何實無理數α,數列
α(
=1,2,…)對模1是一致分布,即它們的分數部分{
α}(
=1,2,…)在
中一致分布。又如,若多項式
(
)的次數大於或等於1,其係數為實數且至少有一個係數為無理數,則數列
(
)(
=1,2,…)對模1是一致分布。命
,
(
)稱為點列
(1≤
≤
)的偏差。因此,若點集
(
=1,2,…)在
中一致分布,則
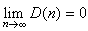 一致分布
一致分布或
(
)=
(1)。偏差是用來刻畫一致分布點集的分布誤差的。關於偏差的重要結果如下:
對於
中任意
個數
(1≤
≤
)及任意正整數
皆有
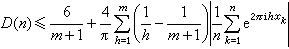 一致分布
一致分布。這基本上是P.愛爾特希和P.圖蘭得到的。
對於
中任意
個點皆有
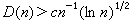 一致分布
一致分布,此處с為一個正的絕對常數。這是K.F.羅特得到的。
一致分布的定義可以推廣到s維歐幾里得空間,此處s≥2。命
表示s維單位立方體,即適合0≤
≤1,1≤
≤s的全體點尣 =(
,
,…,
)。命
(
)=(
(
),
(
),…,
(
))(
=1,2,…)為
中的點集。對於任意
=(
,
,…,
)∈
,命
(
)表示適合下麵條件的
(
)(1≤
≤
)的個數0≤
(
)<
,1≤
≤s,則這
個點的偏差定義為
,
此處|
|=
…
。若
(
)=
(1),則稱點集
(
)(
=1,2,…)在
中一致分布。
外爾判別法及關於偏差的結果,在s維空間都有相應的推廣。
一致分布的定義及外爾判別法還可以推廣到緊緻空間與拓撲群。
一致分布理論中有不少待解決的問題。例如數列e(
=1,2,…)是否對模1為一致分布,就是未解決的著名問題。
參考書目
華羅庚著:《指數和的估計及其在數論中的套用》,科學出版社,北京,1963。
L.Kuipers and H.Niederreiter,Uniform Distribution of Sequences, John Wiley & Sons,NewYork, 1974.