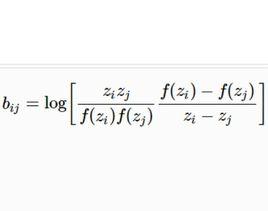基本介紹
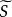 復對稱矩陣
復對稱矩陣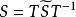 復對稱矩陣
復對稱矩陣復對稱矩陣指a=a(i,j=1,2,…,n)的n階復矩陣A=(a)。任何n階復矩陣相似於復對稱矩陣,任何復對稱矩陣S正交相似於對稱矩陣,即存在正交矩陣T,使,其中
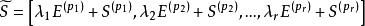 復對稱矩陣
復對稱矩陣是準對角形矩陣,子塊E 是p階單位矩陣,子塊
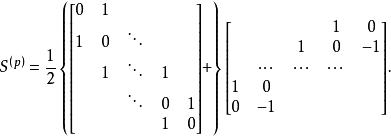 復對稱矩陣
復對稱矩陣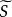 復對稱矩陣
復對稱矩陣稱為復對稱矩陣S的標準形 。
相關分析
矩陣A∈M是對稱的,是指A=A ,在許多場合,所研究的對稱矩陣只有實元素,因而它們是實Hermite矩陣 。
但是,在有些情形,我們要與復對稱矩陣打交道,一個例子是研究複平面中單位圓盤的正則解析映射,如果f(z)是單位圓盤上的正則解析函式,又如果f(z)是適合f(0)=0和f'(0)=1的標準化了的函式,那么,f(z)是一一的(有時稱為單葉的), 若且唯若
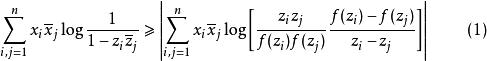 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣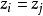 復對稱矩陣
復對稱矩陣對滿足|z|<1的點∈C的所有選擇,點∈C的所有選擇和所有n=1,2,...成立。如果,則右邊的差商可以看作f'(z)。這些稱為Grunsky不等式組的龐雜不等式有很簡單的代數形式
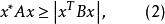 復對稱矩陣
復對稱矩陣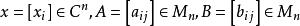 復對稱矩陣
復對稱矩陣其中,
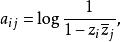 復對稱矩陣
復對稱矩陣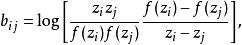 復對稱矩陣
復對稱矩陣應注意的是,A是Hermite矩陣,而B是 復對稱矩陣。
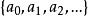 復對稱矩陣
復對稱矩陣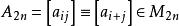 復對稱矩陣
復對稱矩陣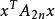 復對稱矩陣
復對稱矩陣另一個自然要產生復對稱矩陣的例子出現在一般的矩問題中。設是給定的複數序列,設n≥1是某個正整數,且定義,注意A是形狀為Hankel矩陣的復對稱矩陣。對x∈C ,我們考慮復二次型,要問是否存在某個固定常數c>0,使得對所有x∈C2 和所有n=1,2,...有
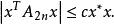 復對稱矩陣
復對稱矩陣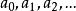 復對稱矩陣
復對稱矩陣根據Nebari定理,這個條件成立, 若且唯若存在一個幾乎處處有界的Lebesgue可測函式F(t): F(t):R→C,它的Fourier係數是已知數;關於F(t)的本質邊界恰好是上述不等式組的常數c。
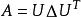 復對稱矩陣
復對稱矩陣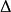 復對稱矩陣
復對稱矩陣在實際套用中復對稱矩陣似乎不像復Hermite(或實對稱)矩陣那樣幾乎經常出現,但是前兩個例子說明,它們還是出現了,雖然復對稱矩陣不一定可對角化,可是復對稱矩陣有一個類似於Hermite 矩陣的譜定理的分解,並且可以用邏輯上類似的方法來證明它,我們首先證明一個與Schur三角分解定理類似的定理,它說明,包括對稱矩陣在內的一類矩陣總可以分解成,其中U是西矩陣,是上三角矩陣,如果,上三角矩陣是對稱的,則它必定是對角矩陣 。
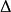 復對稱矩陣
復對稱矩陣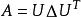 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣定理1 設A∈M是給定的,那么存在西矩陣U∈M和上三角矩陣∈M使得,若且唯若的所有特徵值是非負實數,在這個條件下,的所有主對角元可以選取非負值。
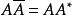 復對稱矩陣
復對稱矩陣每個對稱矩陣A∈M有如下性質:的所有特徵值都是非負的。該特殊形式已包含在上述定理中,人們通常把它歸功於Schur(1945). 但是較早的證明是由Hua(1944),Siegel(1943)和Jacobsen(1939)提出的;而歷史的優先權顯然應該屬於Takagi(1925)。
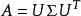 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣 復對稱矩陣
復對稱矩陣推論(Takagi分解) 如果A∈M是對稱矩陣(A=A ),則存在西矩陣U∈M和非負實對角矩陣Σ=diag(σ₁,..σ)使得。U的諸列是由的特徵向量組成的標準正交組,而Σ的相應對角元是的相應特徵值的非負平方根 。