相乘法
這是利用化合價書寫物質化學式的方法它適用於兩種元素或兩種基團組成的化合物,其根據的原理是化合價法則:正價總數與負價總數的代數和為0或正價總數與負價總數的絕對值相等。
相比法
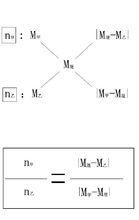 十字交叉法
十字交叉法我們常說十字交叉法實際上是十字交叉相比法,它是一種圖示方法。十字交叉圖示法實際上是代替求和公式的一種簡捷算法,它特別適合於兩總量、兩關係的混合物的計算(即2—2型混合物計算),用來計算混合物中兩種組成成分的比值。
此類問題其實類似於“雞兔同籠”問題,所以解決此類問題首先應該做的就是“一邊倒”。即假設它只是其中一種物質,是什麼情況?之後通過作差就能求比了。
同一物質的甲、乙兩溶液的百分比濃度分別為a%、b%(a%>b%),現用這兩種溶液配製百分比濃度為c%的溶液。問取這兩種溶液的質量比應是多少?
同一物質的溶液,配製前後溶質的質量相等,利用這一原理可列式求解。
設甲、乙兩溶液各取m1、m2克,兩溶液混合後的溶液質量是(m1+m2)。列式
m1a%+m2b%=(m1+m2)c%把此式整理得:m1:m2=(c-b)/(a-c),m1:m2就是所取甲、乙兩溶液的質量比。
為了便於記憶和運算,若用C濃代替a,C稀代替b,C混代替C,m濃代替m1,m
稀代替m2,把上式寫成十字交叉法的一般形式,圖示如下:
圖示中m濃m稀就是所求的甲、乙兩溶液的質量比。
這種運算方法,叫十字交叉法。在運用十字交叉法進行計算時要注意,斜找差數,橫看結果。
原理
就是一種二元一次方程的解法而已。
x + y = 1
ax + by = c
c介於a與b之間,求解:x:y
適用範圍
十字交叉消去法簡稱為十字消去法,它是一類離子推斷題的解法,採用“十字消去”可縮小未知物質的範圍,以便於利用題給條件確定物質,找出正確答案。
例題詳解
十字交叉法的本質就是解二元一次方程的簡便形式,該類題目也可以列方程解,使用該法則的具體方法如下:像A的濃度為10,B的濃度為8,它們的混合物濃度為9,你就可以把9放在中間,把10和8寫在左邊,標上AB,然後分別減去9,可得右邊分別為1和1。此時之比就為1:1 。
(一)混合氣體計算
【例題】在常溫下,將1體積乙烯和一定量的某氣態未知烴混合,測得混合氣體對氫氣的相對密度為12倍,求這種烴所占的體積。
【分析】根據相對密度計算可得混合氣體的平均式量為24,乙烯的式量是28,那么未知烴的式量肯定小於24,式量小於24的烴只有甲烷,利用十字交叉法可求得甲烷是1/2體積
(二)原子含量計算
【例題】溴有兩種核素,在自然界中這兩種核素大約各占一半,已知溴的原子序數是35,原子量是80,則溴的兩種同位素的中子數分別等於。
(A)79 、81 (B)45 、46 (C)44 、45 (D)44 、46
【分析】兩種同位素大約各占一半,根據十字交叉法可知,兩種同位素原子量與溴原子量的差值相等,那么它們的中子數應相差2,所以答案為D
設兩個中子數分別為X和Y,因為各占一半,所以後面是1:1
X 1
80-35=45
Y 1
45+1=46,45-1=44
(三)溶液配製計算
【例題】某同學欲配製40%的NaOH溶液100克,實驗室中現有10%的NaOH溶液和NaOH固體,問此同學應各取上述物質多少克?
【分析】10%NaOH溶液溶質質量分數為10%,NaOH固體”溶質的質量分數“為100%,40%NaOH溶液溶質的質量分數為40%,利用十字交叉法得:需10%NaOH溶液為2╱3×100=66.7克,需NaOH固體為 1╱3×100=33.3克
(四)混合物反應計算
【例題】現有100克碳酸鋰和碳酸鋇的混合物,它們和一定濃度的鹽酸反應時所消耗鹽酸跟100克碳酸鈣和該濃度鹽酸反應時消耗鹽酸量相同。計算混合物中碳酸鋰和碳酸鋇的物質的量之比。
【分析】可將碳酸鈣的式量理解為碳酸鋰和碳酸鋇的混合物的平均式量,利用十字交叉法計算可得碳酸鋰和碳酸鋇的物質的量之比97:26
(五)數學統計
【例題1】(2007年國家公務員考試題)某高校2006年度畢業學生7650名,比上年度增加2% 。其中本科畢業生比上年度減少2%。而研究生畢業生數量比上年度增加10 %,那么這所高校今年畢業的本科生有多少人?
【分析】根據題意,可以得出上一個年度的學生情況!以下均省略百分號!
本科98\ /8
總和 102
碩士 110/ \4
所以,本科和碩士的比例是2:1.
那么根據題意,上一年度的畢業生有7650÷1.02=7500
而本科:碩士=2:1
所以上一年度有本科7500*2/3=5000
本年度本科生減少了2%,所以就有5000×98%=4900。
【例題2】某班一次數學測試,全班平均91分,其中男生平均88分,女生平均93分,則女生人數是男生人數的多少倍?( )
A. 0.5 B. 1 C. 1.5 D. 2
十字交叉法:
故答案為:C

