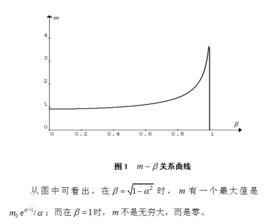
質速關係式
靜質量 m和相對論質量 m兩者的關係式如下:
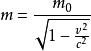 質速關係
質速關係式中 c為光在真空中傳播的速度, v為物體的運動速度。 m與 m兩者之差可以定義為動質量 m= m- m狹義相對論預言,物體的慣性質量隨其運動速度的增加而加大,速度趨於光速時,慣性質量趨於無限大 。
公式推導
在相對論力學中,質能關係等都是由質速關係推導出來的。相對論時空觀認為參考系變換等價於閔氏時空的旋轉,同一個物理過程,其作用量經過參考系變換是不變的。
考慮任意一個物理過程,其作用量為
S= ∫ Ld t= ∫ γ Ld τ
其中 γ為洛倫茲因子, γ=1/(1-v /c ) 。 L為拉格朗日函式, τ為不隨參考系的變換而改變的固有時,所以 γL也是不依賴於參考系選取的常量,令 γL= α,則
L= α/ γ
考慮一個不受任何外力作用的物體做慣性運動,低速條件下,相對論力學退化為牛頓力學形式,有
1 /γ≈1- v /2 c ,故
L≈ α- αv /2 c
現在要求這個形式與牛頓力學形式一致。在牛頓力學中,物體不受任何外力時,
L= T- V= mv /2-0= mv /2
由於在 L上加減任何一個常數,不影響最小作用量原理,因此兩相對比可以得到
α=- mc
於是得到相對論條件下的拉格朗日函式
L=- mc / γ=- mc /(1- v / c )
而物體的動量
p=∂ L/∂ v
最後可得
p= mv/(1- v / c ) = γmv
由此可見,在相對論中,物體的慣性質量不再是個常量 m,而是隨著物體的速度而變化,即
m'= γm
這裡的 m '是相對論質量, m是牛頓力學中的質量,即靜質量 m。將上式中的 m'換成 m, m換成 m,即可得
m= γm
實驗驗證
質速關係有許多實驗事實精確證實其正確性。質能關係 E= mc 和質速關係可以相互導出,荷電粒子的電磁偏轉實驗、回旋加速器的運轉、高速粒子飛行時間的測量、原子光譜精細結構分裂的解釋等都為質速關係提供了證據。原子能發電、核子彈和氫彈的實現都以質能關係為理論基礎 。