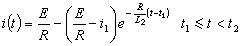動力學普遍方程又稱拉格朗日-達朗伯方程，可表達為：質點系中各質點上的主動力
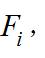動力學普遍方程和慣性力
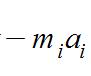動力學普遍方程對於其虛位移
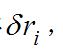動力學普遍方程所作的虛功之總和為零，即
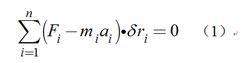動力學普遍方程按照達朗伯原理，對每一質點有：
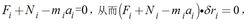動力學普遍方程所以其總和
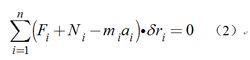動力學普遍方程對理想約束有故
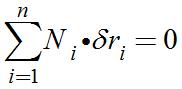動力學普遍方程由式（2）即得式（1）。
套用統一坐標，以表示方向的主動力，則式（1）可寫作：
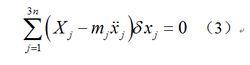動力學普遍方程對於動力學問題，3n個
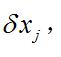動力學普遍方程（j=l，2，…，3n）有約束方程相聯繫，由式（3）不能得出
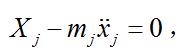動力學普遍方程只能利用約束方程消去與約束方程個數相等的
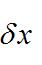動力學普遍方程後，才能使留下的
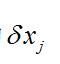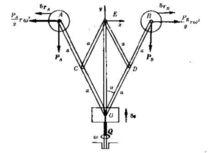
動力學普遍方程前的括弧為零，例如，在離心調速器中，重為P和P（P=P=P）的兩球A和B與一重為Q的套管O用桿
動力學普遍方程連線，且OC=AC=EC=OD=DE=DB=a，略去桿重不計，則此機構可看成由三個質點A，B與0組成。令
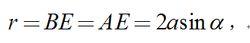動力學普遍方程則當機構以角速度繞軸轉動時，動力學普遍方程可寫為：
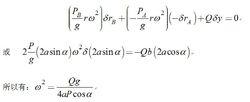動力學普遍方程參考文獻
1、詞條作者：汪家訸．《中國大百科全書》74卷（第一版）力學 詞條：動力學普遍方程：中國大百科全書 出版社，1987 ：118頁．
