原理
達朗伯
求解有約束質點系動力問題的一個原理,是法國數學家J.le R.達朗伯於1743年最先提出的,因而得名。對一個質點,這原理的數學表達式為:
Fi+Ni-miai=0, (1)
式中Fi為加於質量mi的質點的主動力;Ni為限制這質點的約束力(見約束);ai為這質點的加速度。
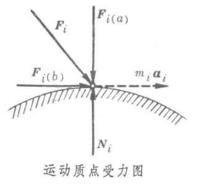
達朗伯把主動力拆成兩個分力 Fi=F+F。其中一個力F與約束力Ni平衡,另一個力F用來產生miai(見圖), 即
F+Ni=0 (2)
和F=miai。故有:F=Fi-F=Fi-miai。(3)
將式(3)代入式(2),即得式(1)。後來的力學家把-miai稱為慣性力,附加在質點上。這樣,式(1)在形式上與靜力學的平衡方程一致,可以敘述為:"質點系的每一個質點所受的主動力Fi、約束力Ni和慣性力-miai成為一平衡力系。"但是,靜力學中構成平衡力系的都是外界物體對質點的作用力,而慣性力並不是外加的。所以,慣性力是一種為了便於解決問題而假設的"虛擬力"。
影響
不論達朗伯本人對式(1)作何種解釋,等式兩邊只是一種數值關係,其結果與從牛頓運動方程Fi+Ni=miai中把miai移項完全相同。但是,把-miai看成慣性力並把式 (1)看成平衡(實際不平衡)的觀點所引入的動靜法和機械學中的動平衡,對力學的發展則發生積極的影響。
事實上,在跟著質點運動的非慣性坐標系的觀察者認為,慣性力是存在的,而且可以測量。例如在垂直方向加速上升的火箭中的太空人,他對座位壓力大於重力。
A.愛因斯坦創立的廣義相對論認為慣性力完全與萬有引力等價;愛因斯坦用升降機說明兩者是不能區分的。因此,從廣義相對論的角度看,慣性力是真實的力。