角動量定理
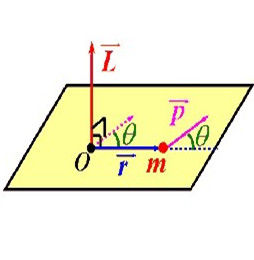
角動量定理，又稱動量矩定理。質點系對一點（或一軸）的角動量對時間的導數等於外力系對此點（或此軸）的主矩，廣泛用於處理剛體定點（或軸）轉動問題。角動量定理可表達成：dlq外dt＝muo角動量的量綱為ml2t－1。
基本信息
- 中文名稱：角動量定理
- 外文名：theory of angular momentum
- 別稱：動量矩定理
- 適用領域範圍：處理剛體定點
簡介
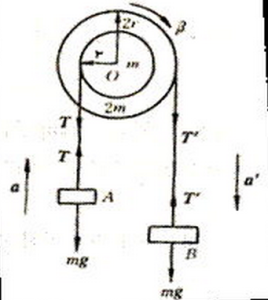角動量定理角動量定理theoryofangularmomentum表述角動量與力矩之間關係的定理。對於質點，角動量定理可表述為：質點對固定點的角動量對時間的微商，等於作用於該質點上的力對該點的力矩。對於質點系，由於其內各質點間相互作用的內力服從牛頓第三定律，因而質點系的內力對任一點的主矩為零。利用內力的這一特性，即可導出質點系的角動量定理：質點系對任一固定點O的角動量對時間的微商等於作用於該質點系的諸外力對O點的力矩的矢量和。即，式中ri、mi和vi分別為質點系中第m個質點關於O點的矢徑、質量和速度矢量。這一定理中的O點必須固定。在一般情況下，對於動點，這個定理不成立；但質點系的質心例外，關於質心的角動量定理為：質點系對於質心C的角動量，它對時間的微商等於作用在質點系的外力系對質心C的主矩Mσ，即式中r媴為質點系中第i個質點對質心的矢徑。 套用
由此可見，描述質點系整體轉動特性的角動量只與作用於質點系的外力有關，內力不能改變質點系的整體轉動情況。動量矩定理可用來解決質點系動力學中與轉動有關的問題。一般情況下，對於O點是動點的，這個定理不成立，但O點是質點系的質心時例外。