介紹
 力的分解
力的分解如果一個力作用於某一物體上,它對物體產生的效果跟另外幾個力同時作用於同一物體而共同產生的效果相同,這幾個力就是那個力的分力。
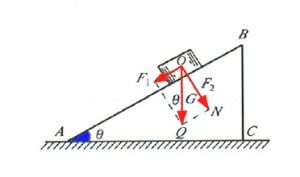
例如,在木板上固定兩根橡皮繩,並在兩繩結點處繫上兩根細線。如右圖所示,用一豎直向下的力F把結點拉至某一位置O,注意觀察拉力F所產生的效果。接著,用沿BO方向的拉力F1專門拉伸OB,沿AO方向的拉力F2專門拉伸OA,當F1、F2分別為適當值時,結點也被拉至位置O。F1、F2共同作用的效果與F作用的效果相同,F1、F2就叫做拉力F的分力。求一個力的分力叫做力的分解。在力的分解中,被分解的那個力(合力)是實際存在的,有對應的施力物體;而分力則是構想的幾個力,沒有與之對應的施力物體。
如何分解
力的分解是力的合成的逆運算,同樣遵循平行四邊形定則(三角形法則,很少用):把一個已知力作為平行四邊形的對角線,那么與已知力共點的平行四邊形的兩條鄰邊就表示已知力的兩個分力。然而,如果沒有其他限制,對於同一條對角線,可以作出無數個不同的平行四邊形。
為此,在分解某個力時,常可採用以下兩種方式:
①按照力產生的實際效果進行分解——先根據力的實際作用效果確定分力的方向,再根據平行四邊形定則求出分力的大小。②根據“正交分解法”進行分解——先合理選定直角坐標系,再將已知力投影到坐標軸上求出它的兩個分量。
關於第②種分解方法,我們將在這裡重點講一下按實際效果分解力的幾類典型問題:放在水平面上的物體所受斜向上拉力的分解將物體放在彈簧台秤上,注意彈簧台秤的示數,然後作用一個水平拉力,再使拉力的方向從水平方向緩慢地向上偏轉,台秤示數逐漸變小,說明拉力除有水平向前拉物體的效果外,還有豎直向上提物體的效果。所以,可將斜向上的拉力沿水平向前和豎直向上兩個方向分解。斜面上物體重力的分解所示,在斜面上鋪上一層海綿,放上一個圓柱形重物,可以觀察到重物下滾的同時,還能使海綿形變有壓力作用,從而說明為什麼將重力分解成F1和F2這樣兩個分力。
定則
三角形
即將兩個分力首尾相接,則合力就是由f1首端指向f2尾端的有向線段.
把兩個矢量首尾相接從而求出和矢量的方法,叫做三角形定則。
力是矢量,求兩個力的合力時,不能簡單把兩個力相加,而按三角形定則來確定力的大小和方向。
平行四邊形
兩個力合成時,以表示這兩個力的線段為鄰邊作平行四邊形,這兩個鄰邊之間的對角線就代表合力的大小和方向,這就叫做平行四邊形定則(parallelogramrule)。
平行四邊形定則是一切矢量合成的普遍適應性定則,如速度、加速度、位移等。若一條直線上兩個力合成時,可以通過規定正方向的辦法,把力的合成運算轉化成代數運算。
分解法
 力的分解
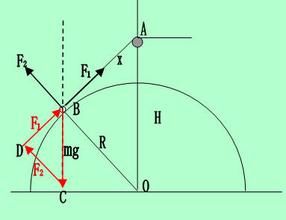
力的分解①先進行受力分析(這一點很重要),接著正確選擇直角坐標系,一般選共點力的作用點為原點,水平方向或物體運動的加速度方向為X軸,使儘量多的力在坐標軸上。
②正交分解各力,即分別將各力投影在坐標軸上,分別求出坐標軸上各力投影的合力。
Fx=F1x+F2x+…+Fnx,Fy=F1y+F2y+…+Fny
③共點力合力的大小為F=√Fx2+√Fy2(根號下Fx的平方加根號下Fy的平方),合力方向與X軸夾角tank=Fy/Fx(即求出tan值,在和已知的tan值比較,進而得知k的度數)
例:已知:F1,F2為F的分力,F的角度為37,物體重力為G,動摩擦因數為0.5。
求:f的大小,加速度的大小
解:F1=Sin37*FF2=Cos37*F
f=μN=0.5*(G-Sin37*F)F合=F2-f=m*a
a=cos37*F-0.5*(G-Sin37*F)/(G/g)
注;斜面上的重力分解
使物體向下滑的分力=mg·sin角度
正壓力=mg·cos角度