運算法則
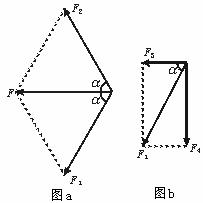
1.力的合成與分解互為逆運算,都符合和平行四邊形法則:如果用表示兩個共點力F1和F2的線段為鄰邊作平行四邊形,那么合力F的大小和方向就可以用F1、F2所夾的角的大小來表示。
(註:已知分力要求合力,叫做力的合成。已知合力要求分力叫做力的分解。)
2.力的合成與分解的法則:平行四邊形法則。即力的合成就是由平行四邊形的兩鄰邊求對角線的問題。力的分解就是由對角線求兩鄰邊的問題。
3.當兩個力的方向相反(即兩個力成一百八十度),其合力最小;反之(即是兩個力成零度)最大。
(註:對力按平行四邊形法則進行分解時要按力的實際效果或正交分解法進行。)
.合力和力的合成:一個力產生的效果如果能跟原來幾個力共同作用產生的效果相同,這個力就叫那幾個力的合力,求幾個力的合力叫力的合成. 2.力的平行四邊形定則:求兩個互成角度的共點力的合力,可以用表示這兩個力的線段為鄰邊作平行四邊形,合力的大小和方向就可以用這個平行四邊形的對角線表示出來。
共點的兩個力F1,F2的合力F的大小,與它們的夾角θ(0≤θ≤π)有關,θ越大,合力越小;θ越小,合力越大,合力可能比分力大,也可能比分力小,F1與F2同向時合力最大,F1與F2反向時合力最小,合力大小的取值範圍是|F1-F2|≤F≤(F1+F2)
多個力求合力的範圍
有n個力,它們合力的最大值是它們的方向相同時的合力,即它們的代數之和,而它們的最小值要分下列兩種情況討論:
①若n個力中的最大力大於其他力的代數之和,則它們合力的最小值是該最大力與其他力代數和的差(此時,所有力在一條直線上,最大力的方向與其他力的方向相反);
②若n個力中的最大力小於其他力的代數之和,則它們合力的最小值是0。
3.三角形法則:求兩個互成角度的共點力F1,F2的合力,可以把F1,F2首尾相接地畫出來,把F1,F2的另外兩端連線起來,則此連線就表示合力F的大小和方向;
4.分力與力的分解:如果幾個力的作用效果跟原來一個力的作用效果相同,這幾個力叫原來那個力的分力.求
 平行四邊形定則
平行四邊形定則一個力的分力叫做力的分解.
5.分解原則:平行四邊形定則.
力的分解是力的合成的逆運算,同樣遵循的平行四邊形定則。
同樣,由力的分解所遵循的平行四邊形定則可知:如不加任何限制而將某個力分解為兩個分力,則可以得到無數種分解的方式,這是毫無意義的。通常作力的分解時所加的限制有兩種:按照力的作用效果進行分解,按照所建立的直角坐標將力作正交分解。
6、正交分解法
物體受到多個力作用時求其合力,可將各個力沿兩個相互垂直的方向直行正交分解,然後再分別沿這兩個方向求出合力,正交分解法是處理多個力作用用問題的基本方法,值得注意的是,對、方向選擇時,儘可能使落在、軸上的力多;被分解的力儘可能是已知力。步驟為:
①正確選擇直角坐標系,一般選共點力的作用點為原點,水平方向或物體運動的加速度方向為X軸,使儘量多的力在坐標軸上。
②正交分解各力,即分別將各力投影在坐標軸上,分別求出坐標軸上各力投影的合力。
Fx=F1x+F2x+…+Fnx
Fy=F1y+F2y+…+Fny
③共點力合力的大小為F=√Fx2=Fy2(根號下Fx的平方加根號下Fy的平方),合力方向與X軸夾角
受力分析
(1)物體受力情況分析的理解:把某個特定的物體在某個特定的物理環境中所受到的力一個不漏,一個不重地找出來,並畫出定性的受力示意圖。對物體進行正確地受力分析,是解決好力學問題的關鍵。
(2)物體受力情況分析的方法:為了不使被研究對象所受到的力與所施出的力混淆起來,通常需要採用“隔離法”,把所研究的對象從所處的物理環境中隔離出來;為了不使被研究對象所受到的力在分析過程中發生遺漏或重複,通常需要按照某種順序逐一進行受力情況分析,而相對合理的順序則是先找重力,再找接觸力(彈力、摩擦力),最後分析其它力(場力、浮力等)。
重力是否有:巨觀物體都計重力,而一些微觀粒子有時不計重力
彈力看四周
分析摩擦力
不忘電磁浮
(3)受力分析的幾個步驟.
①靈活選擇研究對象:也就是說根據解題的目的,從體系中隔離出所要研究的某一個物體,或從物體中隔離出某一部分作為單獨的研究對象,對它進行受力分析.
所選擇的研究對象要與周圍環境聯繫密切並且已知量儘量多;對於較複雜問題,由於物體系各部分相互制約,有時要同時隔離幾個研究對象才能解決問題.究竟怎樣選擇研究對象要依題意靈活處理.
②對研究對象周圍環境進行分析:除了重力外查看哪些物體與研究對象直接接觸,對它有力的作用.凡是直接接觸的環境都不能漏掉分析,而不直接接觸的環境千萬不要考慮進來.然後按照重力、彈力、摩擦力的順序進行力的分析,根據各種力的產生條件和所滿足的物理規律,確定它們的存在或大小、方向、作用點.
③審查研究對象的運動狀態:是平衡態還是加速狀態等等,根據它所處的狀態有時可以確定某些力是否存在或對某些力的方向作出判斷.
④根據上述分析,畫出研究對象的受力分析圖;把各力的方向、作用點(線)準確地表示出來.
(4)物體受力情況分析的依據:在具體的受力分析過程中,判斷物體是否受到某個力的依據通常有如下三個。
①從力的概念判斷,尋找施力物體;
②從力的性質判斷,尋找產生原因;
③從力的效果判斷,尋找是否產生形變或改變運動狀態
概念歸納
1.共點力:物體受到的各力的作用線或作用線的延長線能相交於一點的力
2.平衡狀態:在共點力的作用下,物體保持靜止或勻速直線運動的狀態.
說明:這裡的靜止需要二個條件,一是物體受到的合外力為零,二是物體的速度為零,僅速度為零時物體不一定處於靜止狀態,如物體做豎直上拋運動達到最高點時刻,物體速度為零,但物體不是處於靜止狀態,因為物體受到的合外力不為零.
3.共點力作用下物體的平衡條件:合力為零,即0
說明;
①三力匯交原理:當物體受到三個非平行的共點力作用而平衡時,這三個力必交於一點;
②物體受到N個共點力作用而處於平衡狀態時,取出其中的一個力,則這個力必與剩下的(N-1)個力的合力等大反向。
③若採用正交分解法求平衡問題,則其平衡條件為:FX合=0,FY合=0;
④有固定轉動軸的物體的平衡條件
轉動平衡狀態是靜止或勻速轉動狀態;其共同的物理本質是描述轉動狀態的角速度這一物理量保持恆定;而能夠迫使物體轉動角速度發生變化的只有力矩,所以在有固定轉動軸的物體的平衡條件是:物體所受到的合力矩為零,即=0.
4.力的平衡:作用在物體上幾個力的合力為零,這種情形叫做力的平衡
(1)若處於平衡狀態的物體僅受兩個力作用,這兩個力一定大小相等、方向相反、作用在一條直線上,即二力平衡
(2)若處於平衡狀態的物體受三個力作用,則這三個力中的任意兩個力的合力一定與另一個力大小相等、方向相反、作用在一條直線上
(3)若處於平衡狀態的物體受到三個或三個以上的力的作用,則宜用正交分解法處理,此時的平衡方程可寫成
①確定研究對象;②分析受力情況;③建立適當坐標;④列出平衡方程

