概述
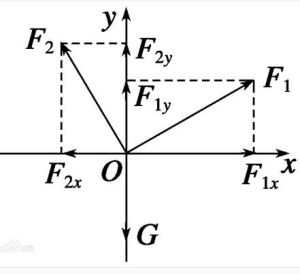
 正交分解法
正交分解法條件意義
求多個共點力合成時,如果連續運用平行四邊形定則求解,一般來說要解若干個斜三角形,一次又一次地求部分合力的大小和方向。計算過程顯得十分複雜,如果採用力的正交分解法求合力,計算過程就顯得較為明了。其基本思想是先分解再合成。
運用條件
物體受到多個方向的外力作用均可使用正交分解法。
運用步驟
第一步,立正交 x、y坐標,這是最重要的一步,x、y坐標的設立,並不一定是水平與豎直方向,可根據問題方便來設定方向,不過x與y的方向一定是相互垂直而正交。
第二步,將題目所給定跟要求的各矢量沿x、y方向分解,求出各分量,凡跟x、y軸方向一致的為正;凡與x、y軸反向為負,標以“一”號,凡跟軸垂直的矢量,該矢量在該軸上的分量為0,這是關鍵的一步。第三步,根據在各軸方向上的運動狀態列方程,這樣就把矢量運算轉化為標量運算;若各時刻運動狀態不同,應根據各時間區間的狀態,分階段來列方程。這是此法的核心一步。
第四步,根據各x、y軸的分量,求出該矢量的大小,一定要表明方向,這是最終的一步。在高中物理學習中,正確套用正交分解法能夠使一些複雜的問題簡單化,並有效的降低解題難度。力的正交分解法在整個動力學中都有著非常重要的作用。
目的原則
目的
把力沿著兩個經選定的互相垂直的方向分解叫力的正交分解法,在多個共點力作用下,運用正交分解法的目的是用代數運算公式來解決矢量的運算。在力的正交分解法中,分解的目的是為了求合力,尤其適用於物體受多個力的情況,物體受到F1,F2,F3…,求合力F時,可把各力沿相互垂直的x軸,y軸分解,則在x軸方向各力的分力分別為 F1x,F2x,F3x…,在y軸方向各力的分力分別為F1y,F2y,F3y….那么在x軸方向的合力Fx = F1x+ F2x+ F3x+ … ,在y軸方向的合力Fy= F2y+ F3y+ F3y+…合力,設合力與x軸的夾角為θ,則在運用正交分解法解題時,關鍵是如何確定直角坐標系。
原則
在靜力學中,以少分解力和容易分解力為原則;在動力學中,以加速方向和垂直加速度方向為坐標軸建立坐標,這樣使牛頓第二定律表達式為:F=ma。
套用舉例
例:已知:F1,F2為F的分力,F的角度為37,物體重力為G,動摩擦因數為0.5.
求:f的大小,加速度的大小解:F1=Sin37*F F2=Cos37*F
f=μN=0.5*(G-Sin37*F) F合=F2-f=m*a
a=(cos37*F-(0.5*(G-Sin37*F))/(G/g)
註:斜面上的重力分解
下滑力=mg·sin角度
正壓力=mg·cos角度
注意
1、力是矢量F′在X軸Y軸上的分矢量F′x和F′y是矢量,分量為正值表示分矢量的方向跟坐標軸的方向相同,分量為負值表示分矢量的方向跟坐標軸的方向相反。2、確定矢量正交分量的坐標軸,不一定是取豎直方向和水平方向。例如,分析物體在斜面上的受力情況,一般選取x軸與斜面平行,y軸與斜面垂直。坐標軸的選取是以使問題的分析簡化為原則。通常選取坐標軸的方法是:選取一條坐標軸與物體運動的加速度的方向相同(包括處理物體在斜面上運動的問題),以求使物體沿另一條坐標軸的加速度為零,這樣就可得到外力在該坐標軸上的分量之和為零,從而給解題帶來方便。
3、正交分解法適用於求多個力的合力。在分解時,要注意根據實際情況讓儘量多的力落在平面直角坐標系中。